Three dimensional simulation of groundwater exploitation and land subsidence based on variable permeability
-
摘要:
在地面沉降过程中伴随着土体孔隙率和渗透系数的变化, 但在模拟计算中为了降低计算量而忽略其变化, 因而在一定程度上造成模拟结果与实际偏离。为了研究地面沉降数值模拟过程中孔隙率和渗透系数变化对模拟结果的具体影响, 在Biot固结理论的基础上, 耦合了Kozeny-Carman方程, 建立了考虑固结过程中渗透系数变化的三维固结模型。以北京平原区的典型含水层结构为模拟对象, 分别在考虑和忽略渗透系数变化的情况下进行抽水模拟, 发现在考虑渗透系数变化的情况下, 抽水后地层的渗透率体现了不均匀变化, 在抽水井井壁附近渗透系数有所降低;考虑渗透系数变化下的地表最终形变量大于忽略渗透系数变化的情况;忽略渗透系数变化导致的模拟误差在沉降初期较小且具有继续发展的趋势, 中后期较大并逐渐趋于平稳, 且这一误差与抽水量正相关, 与承压含水层压缩模量和渗透系数负相关, 且随着承压含水层厚度的增加呈现先增大后减小的趋势。
Abstract:Porosity and permeability of soil keep on changing during the process of land subsidence. However, these are often ignored in order to reduce the computation in the simulation, thus the simulation results may deviate from the actual situation. In order to examine the influence of variable porosity and permeability on the simulation results of subsidence, a 3D consolidation model considering the variation in permeability during consolidation is established based on the coupling of the Biot consolidation theory and Kozeny-Carman equation. Pumping simulations are carried out under the condition of considering and neglecting the variation of permeability in the typical aquifer structure in the Beijing plain. It is found that the change in the layer permeability after pumping is uneven, and the permeability is reduced near the well wall. Considering the change in permeability, the final deformation of the surface is larger than that of ignoring the variation in permeability. The simulation error caused by neglecting the variation in permeability is smaller and has a tendency to develop in the early stage of settlement, and it is larger and more stable in the middle and later stages. This error is positively correlated with the pumping volume and is negatively correlated with the compression modulus and permeability of confined aquifer. With the increasing thickness of the confined aquifer, the error first increases and then decreases.
-
随着人类社会的快速发展, 地下水资源被大量开采, 尤其是在经济较发达地区, 地下水的长期超采导致地面沉降广泛发育。作为首都的北京市是我国地面沉降发育较为严重的地区之一, 目前仍处于地面沉降快速发展时期, 地面沉降造成的经济损失和社会影响日趋明显[1~2]。地下水的过量开采是导致北京平原区地面沉降广泛发育的主要原因[3~5]。地下水开采引发地面沉降是一个十分复杂的过程, 伴随着地面沉降的发生发展, 土体的孔隙率、渗透系数等参数也在不断地发生变化, 这种变化直接影响着土体的渗流和固结状态, 进而反馈在沉降特征中。但目前大部分地面沉降数值模拟的过程中为了减少计算量, 通常不考虑渗透系数的变化[6~7], 这种近似在小变形的假设下是合理的, 但在现实发育的地面沉降中, 累计沉降量通常达到了几百甚至几千毫米[8~11], 此时忽略其变化所得到的模拟结果明显和实际情况是有差距的。因而很有必要查明渗透固结过程中渗透系数的变化过程并明确忽略其变化对沉降过程及最终沉降量的具体影响, 这对提高地面沉降数值模拟结果的精度具有重要意义。
本文在Biot三维固结模型的基础上, 利用Kozeny-Carman方程对渗透固结过程中渗透系数的变化规律进行描述, 在渗透固结的过程中增加考虑了渗透系数变化的影响因素。并以北京平原的潜水层、第一压缩层及第一承压含水层为模拟对象, 在相同的抽水条件下分别进行了变渗透系数和定渗透系数的模拟工作, 主要研究两种情况下地面沉降发展过程中的差异, 对比二者水头及沉降量的差距, 讨论忽略渗透系数变化引起的误差以及抽水量、地层参数等条件对该误差的影响。
1. 控制方程
数值模拟是研究及预测地面沉降发生发展规律的重要手段[12~15]。1936年Terzaghi和Redulic[16]改进了Terzaghi[17]提出的一维固结理论将其推广到了二位和三维, 但没有考虑在土体固结过程中总应力的变化, 因而通常被称为“假三向固结理论”。Biot[18]提出了著名的Biot固结理论, 这一理论考虑了地下水运动和土体变形的相互作用, 将土体的变形模型和地下水流动模型统一于相同的物理空间, 真正的将一维固结理论推广到了三维空间。在此之后, Biot固结理论在地面沉降的模拟计算方面得到了广泛的应用。
1.1 Biot固结模型
Biot固结理论是在力学平衡、有效应力原理、土体本构关系、几何变形关系和地下水连续性基础上建立起来的, 耦合上述5种关系方程得到Biot固结模型, 其方程组表达式[18]为:
(1) 式中: γ——土的重度/(N·m-3);
γw——水的重度/(N·m-3);
G——土体的剪切模量/Pa;
v——土体的泊松比;
us、vs、ws——x、y、z方向的位移/m;
K——渗透系数/(m·d-1);
t——时间/d;
i——水力坡度;
f——水作用在土颗粒上的渗透力/N。
其中的未知量是渗透力f和各方向的位移量, 它们都是x、y、z坐标、水头和时间t的函数, 在给出一定的初始条件和边界条件的情况下即可求解。由式(1)可知渗透系数K将会直接影响土体形变量。
1.2 渗透系数变化模型
在多孔介质渗透系数的变化规律研究及其预测方面, 1880年Seeheim[19]首次提出了多孔介质渗透率与孔隙大小之间的相关关系。之后, 随着相关研究深入, 大量的经验方程、毛细管模型以及统计模型被提出。其中最著名的同时应用最广泛的是Kozeny-Carman方程, 这个方程是由Kozeny在1927年第一次提出, 1937年被Carman[20]修正。之后这个方程被许多学者推广发展成了多种形式, 其中最常见的形式为[21~29]:
(2) 式中: k——多孔介质的渗透率/m2;
n——多孔介质的孔隙度/%;
C——K-C常数;
S——多孔介质的比表面积/(m-1);
在式(2)基础上结合土体变形前后的体应变关系得[21]:
(3) 式中: k——变形后土体渗透率/m2;
k0——土体初始渗透率/m2;
n0——初始孔隙度;
εv——体应变量。
式(3)反映了体应变变化对渗透率的影响关系。
渗透系数与渗透率之间的关系为:
(4) 式中: ρw——水的密度/(kg·m-3);
g——重力加速度/(m·s-2);
μ——水的动力粘滞系数/(Pa·s);
K——渗透系数/(m·s-1)。
利用式(4)将式(3)加入到Biot固结模型的方程组中, 即可耦合计算考虑渗透系数变化情况下的土体变形。
2. 北京平原区模拟背景及模型构建
北京平原区的地层结构是境内多条河流的冲洪积作用形成, 沿西北-东南方向, 由单一地层逐渐过渡为多层地层结构。地下水主要赋存于河流冲洪积作用形成的砂及砂卵砾石中, 一般情况下其成层性较好, 易形成较连续的含水层。基于实际的地质结构和地下水的水力联系, 结合地下水的实际开采情况, 一般将北京平原第四系地层中的含水层和弱透水层划分为4个含水层组。第一含水层组底板埋深25 m左右, 属于潜水, 主要接受大气降水、农田灌溉入渗和河流入渗等补给; 第二含水层组底板埋深为80~100 m, 在开采条件下可得到上部潜水的越流补给, 地下水流动主要以水平径流为主, 排泄主要以农业开采为主, 与第一含水层组水力联系密切; 第三含水层组底板埋深150~180 m, 主要以水平径流为主, 接受侧向补给和越流补给, 开采主要用于生活及工业用水; 第四含水层组底板为第四系的底面, 埋深一般在200~300 m。第二、三、四含水层均属于承压含水层。
本次研究选择北京平原地区冲洪积扇中下部的潜水层、第一压缩层及第一承压含水层组成的地下水系统为模拟对象, 模型中的土体参数及含水层厚度均按照实际情况选取(表 1)。在北京平原地区承压含水层的开采量较大[3, 26], 因而选择第一承压含水层为开采层。
表 1 含水层参数Table 1. Parameters of the aquifer
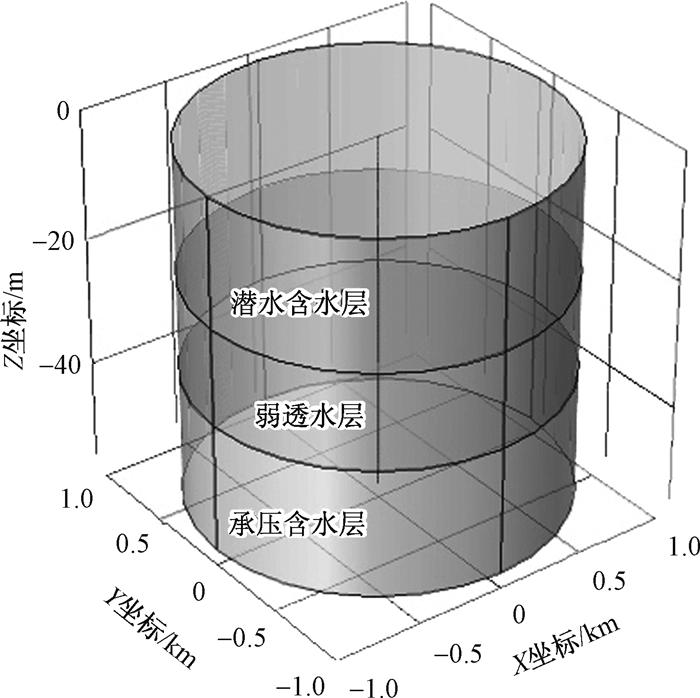
模拟含水层基本结构, 见图 1, 上部第一层为潜水含水层, 厚度为20 m, 底部为承压含水层, 厚度为20 m, 二者之间夹有一层弱透水层, 厚度为15 m。模拟区域是以抽水井为中心, 截面半径为1 000 m, 高为55 m的圆柱形地质体(图 1), 抽水井半径为0.15 m, 贯穿整个地质结构, 滤水段位于穿过两层含水层的井壁处。由于整个模拟过程中只有水头的变化量对于地面沉降具有实际意义, 因而为了简化计算将地表作为基准面, 即地表高程为0 m。
针对上述地质结构和条件分别进行了变渗透系数和定渗透系数的模拟。在正式抽水之前首先给定合理的边界条件计算出合理的初始流场及应力场, 在此基础上开始抽水模拟, 模拟的具体条件见表 2。由于第一阶段仅仅是为了得到合理的初始条件, 并不是本文的研究重点, 后期模拟结果分析中的沉降量及水头变化值不包括第一阶段的变化量。本文模型利用COMSOL Multiphysics进行求解。
表 2 模拟条件Table 2. Conditions of simulation
3. 模拟结果分析
在抽水开始后的一段时间内, 承压水水位不断下降, 同时产生超静孔隙水压力, 并随着排水过程逐渐消散。一段时间后补给量等于排泄量, 各层地下水水位保持不变, 此时超静孔隙水压力消散殆尽, 在整个消散过程中伴随着土体的固结变形, 超静孔隙水压力为零时, 地下水系统达到另一个稳定状态。
通过多次模拟对比分析发现, 抽水作用下的渗透固结过程在开始抽水后400 h时已基本完成, 此时各参数及形变量已达到变化终点, 形成稳定状态。
3.1 渗透系数变化
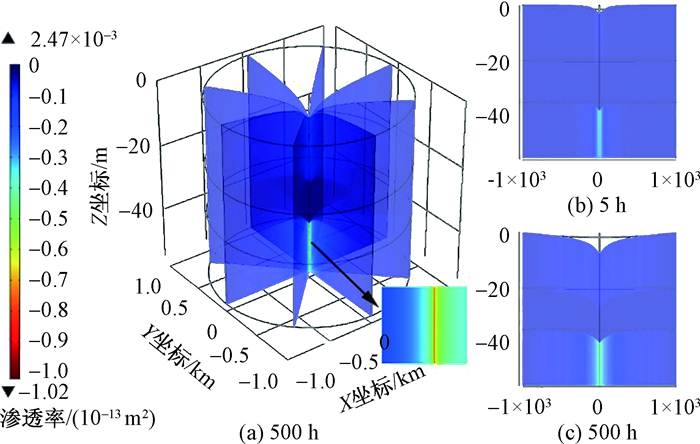
由于假设在模拟过程中的流体性质不发生变化, 所以渗透系数的变化规律与渗透率一致。抽水的初始时刻同一水平面上渗透率相等, 在变渗透系数的情况下抽水初期承压含水层井壁附近渗透率开始降低(图 2), 随着不断抽水渗透率降低的范围逐渐扩大, 但扩大的速度逐渐减小, 最终趋于稳定。
渗透系数的变化是由于抽水过程中靠近井壁处的水头首先开始降低, 土体的有效应力增加, 靠近井壁的土体首先被压缩, 土体变密实且孔隙率减小, 进而导致靠近井壁的土体渗透率首先减小。随着抽水的进行, 水头降低范围逐渐扩大, 土体压缩范围也增大, 所以渗透率减小范围也随之延伸, 渗透系数的变化规律在一定程度上和水头变化的过程是一致的。上述考虑土体固结变形过程中渗透系数变化的模拟结果与实际情况相符[27]。
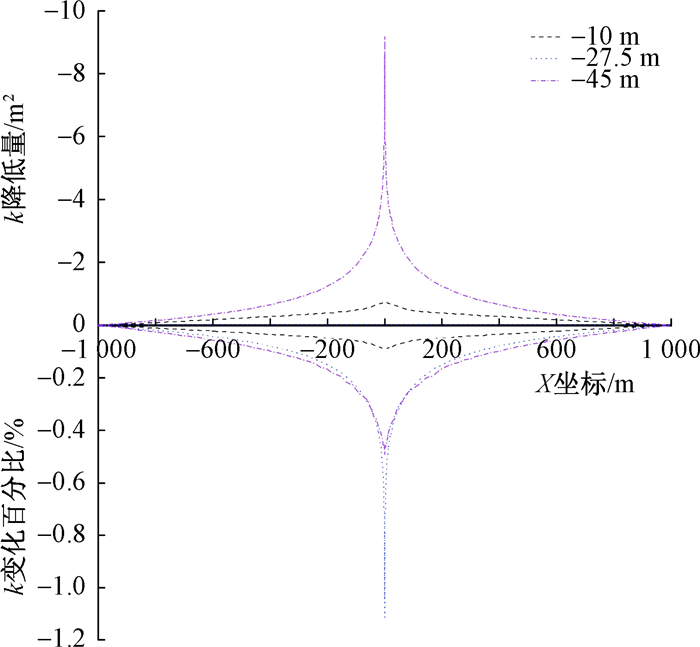
图 3分别选取了位于潜水含水层深度10.0 m和弱透水层中部深度27.5 m处过抽水井的截线, 将其上500 h时渗透率的变化曲线与承压含水层中深度为45.0 m处截线上的渗透率变化曲线进行对比, 发现潜水含水层和弱透水层在靠近井壁附近的范围渗透率有所降低, 但减少量较小。这是由于在承压含水层抽水, 各层之间的水头差增大, 导致越流补给, 造成潜水层及弱透水层内的水头降低, 进而被压缩且渗透率减小。综上所述, 随着抽水的进行, 地层的渗透率体现出了不均匀变化的现象。
3.2 沉降变化
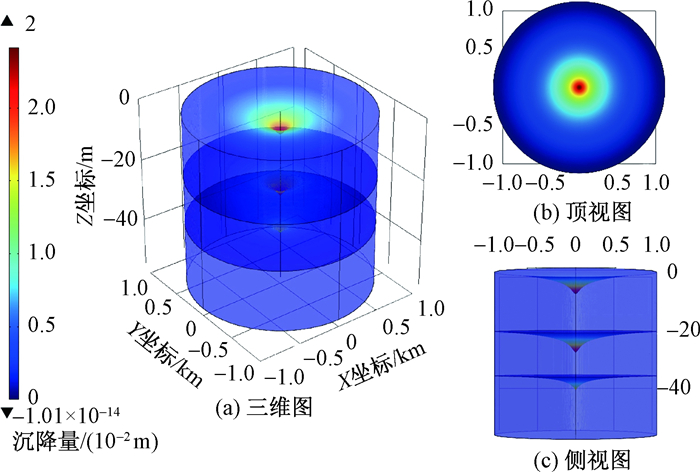
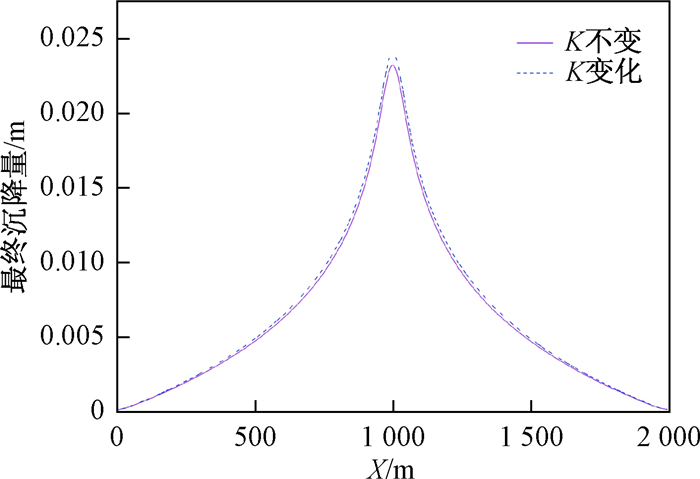
由于抽水作用在地表形成以抽水井为中心的沉降漏斗(图 4)。对比两次模拟结果发现, 在沉降漏斗中心部位, 考虑渗透系数变化时的最终沉降量大于不考虑渗透系数变化时的最终沉降量(图 5), 前者的最终沉降量是24.126 mm, 后者的最终沉降量是23.233 mm, 二者相差0.893 mm, 这一差值是由于模拟中不考虑渗透固结过程中渗透系数的变化造成的误差。在沿沉降漏斗中心指向边界的方向上, 二者沉降量之差逐渐减小。这是由于随着抽水的进行, 在承压含水层井壁附近的土体渗透系数减小, 导致在抽水量相同的情况下水头下降速度变快且稳定时水头降低幅度较大, 即孔隙水压力减小幅度较大, 导致有效应力增加量较大, 所以土体的最终压缩量较不考虑渗透系数变化时大。在实际的模拟应用中, 变渗透系数的模拟结果更接近实际情况, 忽略渗透固结过程中渗透系数的变化会造成得到的最终沉降量偏小, 具体偏小的程度与抽水量、土体性质以及地层结构有密切的联系, 因而在精度要求较高的模拟工作中应当考虑渗透系数的变化, 否则会造成最终沉降量的错误估计, 可能引发严重后果。
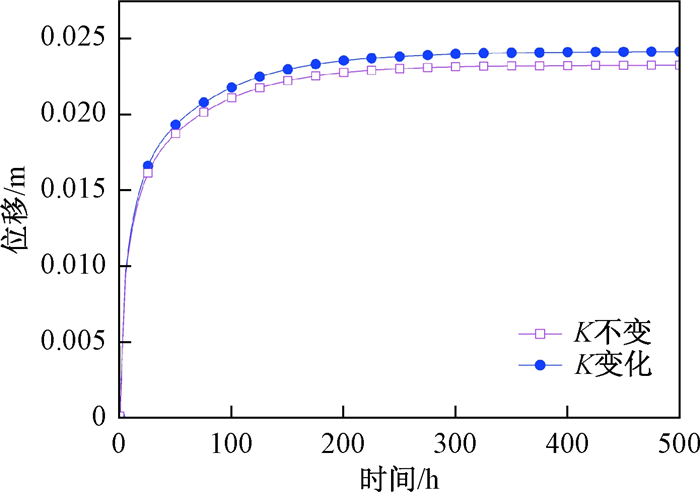
由图 6可以看出在抽水初期两种情况下沉降量的差距较小, 之后随着抽水的继续二者的沉降量之差逐渐增大, 沉降稳定后二者之差也达到稳定状态。所以在沉降初期忽略渗透系数变化对沉降量计算结果造成的误差较小, 但有继续增大的趋势, 中后期造成的累计误差较大并逐渐趋于稳定。
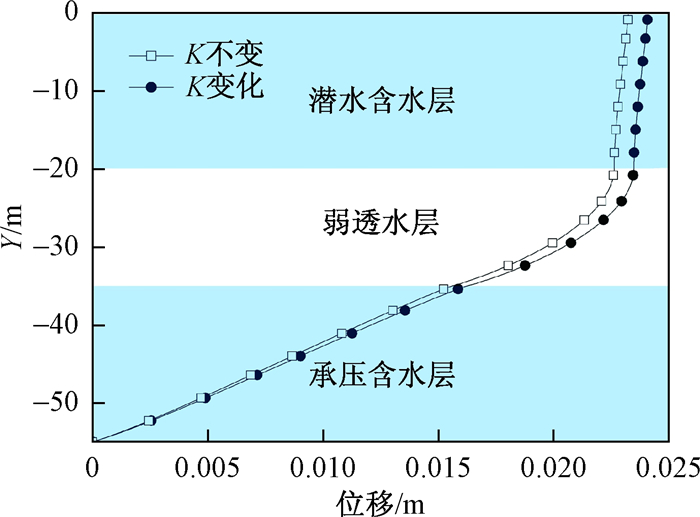
通过对比各地层的沉降量(图 7), 发现沉降量在承压含水层和潜水层中与埋深线性相关, 在弱透水层中呈非线性变化。承压含水层的压缩量最大, 弱透水层次之, 潜水含水层的压缩量最小, 在一定程度上说明离开采层越近的地层压缩量越大, 忽略渗透系数造成的沉降误差也随着沉降量的增大而增大。
3.3 各因素对沉降量及误差的影响
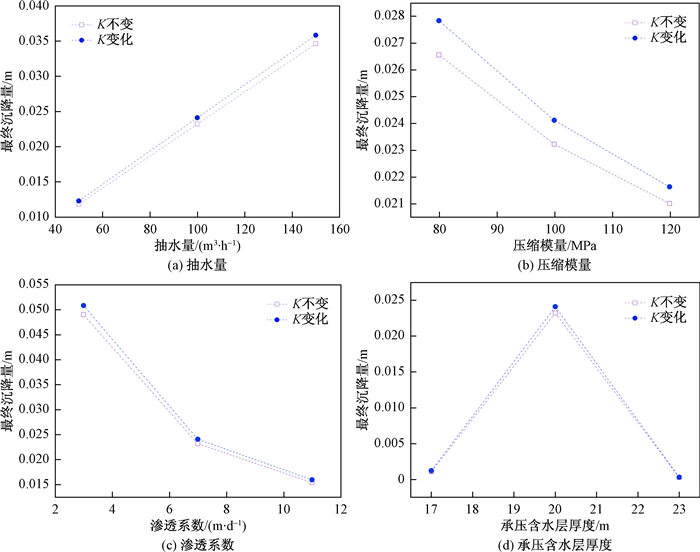
为了进一步研究忽略渗透系数变化导致的沉降误差与抽水量、地层参数及结构之间的具体关系, 在上述模型的基础上针对抽水量和承压含水层的压缩模量、渗透系数以及含水层厚度分别进行了单因素的变化模拟。
模拟结果显示(图 8), 随着抽水量的增加, 在最终沉降量增加的同时, 忽略渗透系数变化造成的误差也随之增大。随着承压含水层压缩模量和渗透系数的增加, 最终沉降量均有所减小, 与此同时忽略渗透系数变化造成的误差也随之减小。值得注意的是沉降量与承压含水层厚度之间并不呈现简单的正相关或负相关关系, 而是承压含水层厚度适中时最终沉降量和误差都最大, 这是由于部分压缩量较小的弱透水层被部分压缩量较大的承压含水层代替后, 导致压缩量增大; 但同时承压含水层厚度增大也直接导致过水断面变大, 因而在外部定水头条件下使得补给量变大, 模拟区内水头降深减小, 进而导致沉降量减小, 在上述两种机理的作用下, 最终沉降量随着含水层厚度的增大呈现先增大后减小的趋势。
由对比可以发现忽略渗透系数变化所造成的沉降误差与最终沉降量呈正相关关系。
4. 结论
利用Biot模型和K-C模型耦合得到变渗透系数固结模型, 针对北京平原区典型含水层结构进行抽水引发地面沉降的模拟, 通过对比分析得到结论:
(1) 在考虑渗透系数变化的情况下, 在抽水井井壁附近, 渗透系数有所降低, 且在远离井壁的方向上渗透系数的下降量逐渐减小, 随着抽水时间的增加变化量逐渐减小, 进而趋于稳定。随着抽水的进行, 地层的渗透率体现了不均匀变化的现象。
(2) 考虑渗透系数变化下的地表最终形变量大于忽略渗透系数变化的情况, 具体差距的大小与抽水量、土体的力学参数及含水层结构有密切的关系, 所以在精度要求较高的模拟中不可以轻易忽略渗透系数在渗透固结过程中的变化, 否则会造成较大误差。
(3) 忽略渗透系数变化导致的模拟误差在沉降初期较小且具有继续发展的趋势, 中后期较大并逐渐趋于平稳。
(4) 忽略渗透系数变化造成的沉降误差随着沉降量的增大而增大, 且与抽水量呈正相关, 与承压含水层压缩模量和渗透系数负相关, 随着承压含水层厚度的增加呈现先增大后减小的趋势。
-
表 1 含水层参数
Table 1 Parameters of the aquifer

表 2 模拟条件
Table 2 Conditions of simulation

-
[1] 贾三满, 王海刚, 罗勇, 等. 北京市地面沉降发展及对城市建设的影响[J]. 城市地质, 2007, 1(4): 19-23. DOI: 10.3969/j.issn.1007-1903.2007.04.005 JIA S M, WANG H G, LUO Y, et al. The impacts of land subsidence on city build of Beijing[J]. City Geology, 2007, 1(4): 19-23. (in Chinese) DOI: 10.3969/j.issn.1007-1903.2007.04.005
[2] 杨建民, 纪森林. 抽水导致区域性地面沉降中的s-lnr线性关系[J]. 岩土工程学报, 2016, 38(9): 1606-1614. YANG J M, JI S L. Linear s-lnr relation of regional land subsidence induced by groundwater withdrawal[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(9): 1606-1614. (in Chinese)
[3] 王祎萍. 北京市超量开采地下水引起的地面沉降研究[J]. 勘察科学技术, 2004(5): 46-49. DOI: 10.3969/j.issn.1001-3946.2004.05.013 WANG Y P. Study on land subsidence caused by overexploiting groundwater in Beijing[J]. Site Investigation Science and Technology, 2004(5): 46-49. (in Chinese) DOI: 10.3969/j.issn.1001-3946.2004.05.013
[4] 杨勇, 郑凡东, 刘立才, 等. 北京平原区地下水水位与地面沉降关系研究[J]. 工程勘察, 2013, 41(8): 44-48. YANG Y, ZHENG F D, LIU L C, et al. Study on the correlation between groundwater level and ground subsidence in Beijing plain areas[J]. Geotechnical Investigation & Surveying, 2013, 41(8): 44-48. (in Chinese)
[5] 周毅, 罗郧, 郭高轩, 等. 冲洪积平原地面沉降特征及主控因素——以北京平原为例[J]. 地质通报, 2016, 35(12): 2100-2110. ZHOU Y, LUO Y, GUO G X, et al. A study of the characteristics of land subsidence and the main control factors in the alluvial plain: a case study of Beijing plain[J]. Geological Bulletin of China, 2016, 35(12): 2100-2110. (in Chinese)
[6] 吴意谦, 朱彦鹏. 考虑侧向变形下抽降潜水引起地面沉降的计算[J]. 华中科技大学学报(自然科学版), 2016, 44(4): 116-120. WU Y Q, ZHU Y P. Calculation of settlement considering lateral deformation due to pumping of phreatic aquifer[J]. J Huazhong Univ of Sci & Tech(Natural Science Edition), 2016, 44(4): 116-120. (in Chinese)
[7] 吴意谦, 朱彦鹏. 考虑疏干带非饱和土影响下基坑降水引起地面沉降的计算[J]. 工程力学, 2016, 33(3): 179-187. WU Y Q, ZHU Y P. Calculation of settlement considering unsaturated soil influence on the dewatering of foundation pits[J]. Engineering Mechanics, 2016, 33(3): 179-187. (in Chinese)
[8] 田芳, 郭萌, 罗勇, 等. 北京地面沉降区土体变形特征[J]. 中国地质, 2012, 39(1): 236-242. DOI: 10.3969/j.issn.1000-3657.2012.01.023 TIAN F, GUO M, LUO Y, et al. The deformation behavior of soil mass in the subsidence area of Beijing[J]. Geology in China, 2012, 39(1): 236-242. (in Chinese) DOI: 10.3969/j.issn.1000-3657.2012.01.023
[9] 张雯, 宫辉力, 陈蓓蓓, 等. 北京典型区地面沉降演化特征与成因分析[J]. 地球信息科学学报, 2015, 17(8): 909-916. ZHANG W, GONG H L, CHEN B B, et al. Evolution and genetic analysis of land subsidence in Beijing typical area[J]. Geo Information Science, 2015, 17(8): 909-916. (in Chinese)
[10] 姜洪涛. 苏锡常地区地面沉降及其若干问题探讨[J]. 第四纪研究, 2005, 25(1): 29-33. JIANG H T. Problems and discussions in the study of land subsidence in the suzhou-wuxi-changzhou area[J]. Quaternary Sciences, 2005, 25(1): 29-33. (in Chinese)
[11] 胡蓓蓓, 姜衍祥, 周俊, 等. 天津市滨海地区地面沉降灾害风险评估与区划[J]. 地理科学, 2008, 28(5): 693-697. DOI: 10.3969/j.issn.1000-0690.2008.05.018 HU B B, JANG Y X, ZHOU J, et al. Assessment and zonation of land subsidence disaster risk of Tianjin Binhai area[J]. Scientia Geographica Sinica, 2008, 28(5): 693-697. (in Chinese) DOI: 10.3969/j.issn.1000-0690.2008.05.018
[12] 陈崇希, 裴顺平. 地下水开采-地面沉降模型研究[J]. 水文地质工程地质, 2001, 28(2): 5-8. CHEN C X, PEI S P. Study on model of groundwater exploitation and ground subsidence[J]. Hydrogeology & Engineering Geology, 2001, 28(2): 5-8. (in Chinese)
[13] 沈孝宇, 孙愫文, 周国云, 等. 宁波城市地面沉降物理数学模型及沉降预测[J]. 地球科学, 1989, 14(2): 135-144. SHEN X Y, SUN S W, ZHOU G Y, et al. Physical mathematics model and prediction on subsidence of Ningbo city[J]. Earth Science, 1989, 14(2): 135-144. (in Chinese)
[14] 陈武, 裴万胜, 李双洋, 等. 饱和多孔介质流-固耦合的数值模型及工程应用[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3346-3354. CHEN W, PEI W S, LI S Y, et al. Numerical simulation and engineering application of solid-fluid coupled model for saturated porous media[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(Sup2): 3346-3354. (in Chinese)
[15] 金玮泽, 骆祖江, 陈兴贤, 等. 地下水渗流与地面沉降耦合模拟[J]. 地球科学-中国地质大学学报, 2014, 39(5): 611-619. JIN W Z, LUO Z J, CHEN X X, et al. Coupling simulation of groundwater seepage and land subsidence[J]. Earth Science Journal of China University of Geosciences, 2014, 39(5): 611-619. (in Chinese)
[16] 安庆军. 太沙基固结理论的若干问题研究[D]. 南京: 南京工业大学, 2007. AN Q J. Study on some problems of Terzaghi consolidation theory[D]. Nanjing: Nanjing University of Technology, 2007. (in Chinese)
[17] Terzaghi K. Principle of soil mechanics IV: settlement and consolidation of Clay[J]. Engineering News Record, 1925, 5(8): 874-878.
[18] Biot M A. General theory of three-dimensional consolidation[J]. Journal of Applied Physics, 1941, 38(12): 155-164.
[19] Seelheim F. Methoden zur bestimmung der durchlässigkeit des bodens[J]. Zeitschrift für Analytische Chemie, 1880, 19(1): 387-402.
[20] Carman P C. Fluid flow through granular beds[J]. Transactions-Institution of Chemical Engineeres, 1937, 15: 150-166.
[21] 刘波, 张功, 江永华, 等. 基于变渗透系数的深基坑单井抽水沉降研究[J]. 工程地质学报, 2014, 22(6): 1123-1127. LIU B, ZHANG G, JIANG Y H, et al. Settlement research on single pumping well of foundation pit using changeable permeability coefficient model[J]. Journal of Engineering Geology, 2014, 22(6): 1123-1127. (in Chinese)
[22] 刘江涛, 廖东良, 葛新民. 基于Kozeny-Carman方程的水相相对渗透率计算方法[J]. 科学技术与工程, 2012, 12(29): 7500-7504. LIU J T, LIAO D L, GE X M. Water Phase Relative Permeability Calculation Based on Kozeny-Carman Equation[J]. Science Technology and Engineering, 2012, 12(29): 7500-7504. (in Chinese)
[23] 徐鹏, 邱淑霞, 姜舟婷, 等. 各向同性多孔介质中Kozeny-Carman常数的分形分析[J]. 重庆大学学报, 2011, 34(4): 78-82. XU P, QIU S X, JIANG Z T, et al. Fractal analysis of Kozeny-Carman constant in the homogenous porous media[J]. Journal of Chongqing University, 2011, 34(4): 78-82. (in Chinese)
[24] 郑斌, 李菊花. 基于Kozeny-Carman方程的渗透率分形模型[J]. 天然气地球科学, 2015, 26(1): 193-198. ZHENG B, LI J H. A New fractal permeability model for porous media based on Kozeny-Carman equation[J]. Natural Gas Geoscience, 2015, 26(1): 193-198. (in Chinese)
[25] Dvorkin J, Gvirtzman H, Nur A. Kozeny-Carman Relation for a Medium with Tapered Cracks[J]. Geophysical Research Letters, 1991, 18(5): 877-880.
[26] Zhu L, Gong H, Li X, et al. Land subsidence due to groundwater withdrawal in the northern Beijing plain, China[J]. Engineering Geology, 2015, 193: 243-255.
[27] 王非, 缪林昌, 黎春林. 抽水地面沉降中含水层渗流变形耦合模型研究[J]. 铁道工程学报, 2011(7): 1-5. WANG F, MIAO L C, LI C L. Study on coupled model for aquifer seepage deformation during pumped ground subsidence[J]. Journal of Railway Engineering Society, 2011(7): 1-5. (in Chinese)
[28] 熊小锋, 施小清, 吴剑锋, 等. 弹塑性变形条件下抽水引起的地面沉降三维数值模拟[J]. 水文地质工程地质, 2017, 44(2): 151-159. https://www.swdzgcdz.com/article/id/20170223 XIONG X F, SHI X Q, WU J F, et al. 3D numerical simulation of elas to-plastic land subsidence induced by groundwater pumping[J]. Hydrogeology & Engineering Geology, 2017, 44(2): 151-159. (in Chinese) https://www.swdzgcdz.com/article/id/20170223
[29] 苏晨, 崔亚莉, 邵景力, 等. 基于理论法的地面沉降数值模型进展[J]. 水文地质工程地质, 2014, 41(6): 147-152. https://www.swdzgcdz.com/article/id/20140625 SU C, CUI Y L, SHAO J L, et al. Advances in numerical models of land subsidence based on comprehensive theories[J]. Hydrogeology & Engineering Geology, 2014, 41(6): 147-152. (in Chinese) https://www.swdzgcdz.com/article/id/20140625
-
期刊类型引用(12)
1. 姜伏伟,唐书君,邓晓飞,李振超,张发旺,尹鸿远. 基坑施工抽水诱发土体渗透破坏的临界抽水量预测. 水文地质工程地质. 2025(01): 53-61 .  本站查看
本站查看
2. 刘贺. 新水情驱动的北京冲洪积平原地面沉降演化特征及分层越流研究. 地质论评. 2025(02): 439-451 .  百度学术
百度学术
3. 单强,汪洋,马丙太,王颖,梁爽,陈社明. 基于可拓理论的唐山市平原区地面沉降危险性评价. 河南科学. 2024(02): 232-241 .  百度学术
百度学术
4. 普拉提·苏力坦. 阿克苏地区地下水渗透系数变化特征分析. 地下水. 2023(02): 61-63 .  百度学术
百度学术
5. 汪洋,单强,马丙太,王锦彪,王颖,董明奇. 冀东平原地面沉降影响因素及易发性评价——以唐山市平原区为例. 人民长江. 2023(04): 150-156 .  百度学术
百度学术
6. 孟世豪,崔亚莉,田芳,罗勇,石鸿蕾. 基于MODFLOW-SUB建立变渗透系数的地下水流-地面沉降模型. 吉林大学学报(地球科学版). 2022(02): 550-559 .  百度学术
百度学术
7. 党发宁,宋靖宇,周玫,张乐. 饱和土的变渗透系数固结理论及其合理性验证. 中国水利水电科学研究院学报(中英文). 2022(06): 506-515 .  百度学术
百度学术
8. 李静伟,许成顺,罗文林,钟紫蓝. 地下水开采引起的地面沉降计算方法及分析. 地下空间与工程学报. 2020(04): 1210-1218 .  百度学术
百度学术
9. 刘蓉,曹国亮,赵勇,陆垂裕,孙青言,严聆嘉,彭鹏. 地面沉降对含水层参数及给水能力的影响研究. 水文地质工程地质. 2019(03): 47-54 .  本站查看
本站查看
10. 王金淑,吴光,赵志明,饶鸿. 贵州贵定尖山营特大桥基础异常升降成因探讨. 水文地质工程地质. 2019(04): 134-141+158 .  本站查看
本站查看
11. 吴静红,程刚,施斌,顾凯,蒋娜. 土层回弹变形特性及回弹潜力试验研究. 高校地质学报. 2019(04): 495-501 .  百度学术
百度学术
12. 宁迪,骆祖江,葛伟亚,贾军元. 江阴南部地区建筑荷载和地下水开采与地面沉降耦合研究. 地质论评. 2019(06): 1549-1558 .  百度学术
百度学术
其他类型引用(10)




 下载:
下载:
 邮件订阅
邮件订阅 RSS
RSS