Power law correlations between feature parameters of loess landslides
-
摘要:
以天水市麦积区幅为例, 利用最小二乘法的拟合方法, 对黄土滑坡发育特征参数的幂律相依性进行了研究。结果表明：(1)滑坡-累积频率的幂律相依性不仅存在于滑坡面积-累积频率、体积-累积频率间, 还存在于滑坡后缘距离分水岭高程与其发生的累积频率之间；(2)滑坡规模参数幂指数分布特征为面积与长度> 面积与宽度> 体积与面积；运动特征参数幂指数的分布特征为体积与最大垂直滑动距离> 体积与最大水平滑动距离> 面积与最大垂直滑动距离> 面积与最大水平滑动距离；(3)滑坡的等效摩擦系数与滑坡面积、体积的幂函数相关性差, 故而该经验关系式仅能代表趋势特征, 不能作为定量分析的依据。
Abstract:Loess landslides are significant natural hazards in the Loess Plateau. They often result in both human and material losses. In this paper, we first collect information including area, volume, length, width, depth and height in a database of loess landslides from the Maiji district of Tianshui in Gansu Province. The power-law dependence is quantitatively examined and the power law relationships among the feature parameters are explored. Based on the detailed inventory, we model the empirical relationships by adopting least square linear fit between the characteristic parameters for the empirical data which are log-transformed. The results show that (1) the power law correlation of the geological disasters not only exists between the cumulative frequency and area scale as well as volume parameters, it also exists in the area between the cumulative frequency and the height difference between loess landslide rear and watershed slopes. (2) For the scale parameters, the power exponent distribution are as follows: the area and length > the area and width > the volume and area. For the motion parameters, the power exponent distribution are as follows: the volume and maximum vertical sliding distance > the volume and maximum horizontal sliding distance > the area and maximum vertical sliding distance > the area and maximum horizontal sliding distance. (3) There is a bad correlation in the power exponent distribution between the sliding equivalent friction coefficient and the area as well as volume. Therefore, their empirical formula can only indicate the trends, and cannot be used as the basis for quantitative analyses.
-
黄土滑坡作为我国黄土地区最为典型的地质灾害, 具有分布范围广、危害大、成因机理和模式复杂等特点, 通常预测和防治难度较大[1~3]。近年来, 随着黄土地区经济的快速发展, 黄土滑坡数量呈现逐渐增长趋势[4], 开展黄土滑坡预测和风险评价是未来较长时间内需要解决的问题。
天水市麦积区是我国黄土滑坡灾害多发的地区之一。吴玮江等[5]、王念秦等[6]通过对天水市黄土滑坡进行系统性论述, 在黄土滑坡的分类、分布特征和诱发因素等方面取得了重要研究进展;李媛等[7]、田尤等[8]分别对天水市内典型滑坡进行了成因特征和稳定性方面的研究, 为黄土高原区滑坡的防治起到了一定积极作用。这些成果多集中于天水市黄土滑坡空间展布特征或滑坡成因等方面, 对天水市黄土滑坡特征参数间的相互依存关系, 即幂律相依性研究并不多见。
自Per Bak等[9]提出自组织临界状态概念以来, 国内外学者对滑坡的幂律相依性进行了不同程度的研究, 发现滑坡的面积、体积与滑坡发生的累积频率之间, 滑坡面积和体积之间存在幂律相依性[10~13]。就此, 本文以天水市麦积区幅为例, 继续开展黄土滑坡发育特征参数间的幂律相依性研究, 试图建立这些参数之间的经验关系式, 验证并拓宽滑坡幂律规则的适用范围, 以期为黄土滑坡的防治预警、风险评估方面提供借鉴。
1. 研究区概况与研究方法
1.1 研究区概况
天水市麦积区幅位于陇西黄土高原东南部, 渭河及其支流河谷地带, 面积440 km2;行政上主要涉及天水市麦积区和清水县, 少量涉及秦州区。该区西南部为山地地貌, 主要出露下古生界牛头河群片岩、片麻岩;北部受地质沉陷和黄土沉积控制, 形成黄土厚度较大的梁峁地貌;中部小部分地区因受纬向构造带的断裂影响, 形成渭河地堑, 经第四纪河流侵蚀、堆积, 形成渭河河谷地貌。区内最高海拔1 923 m、最低海拔1 061 m, 相对高差862 m。该区属温带半湿润半干旱气候区, 具有气候温和、四季分明、降雨适中等特点, 多年平均气温10.5 ℃, 年平均降雨量600 mm。降雨主要集中在7-9月, 且以暴雨和连阴雨形式为主。
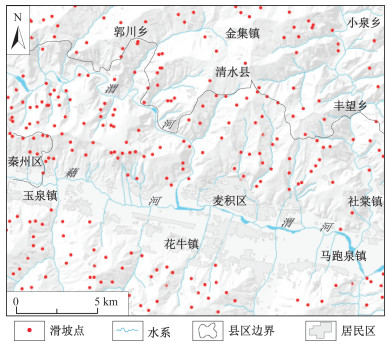
天水市地处六盘山南北地震带中段的天水-武都地震带和秦岭北缘东西地震带中部的天水-兰州地震带的交汇复合部位, 构造上位于青藏高原东北缘近南北向构造带与秦岭构造带交汇区, 沟谷纵横, 地质和地理条件极其脆弱[14], 致使地质灾害发生频率高、分布范围广, 是甘肃省乃至全国最为严重的滑坡受灾地之一。野外调查数据显示, 研究区共发育体积大于1万方的滑坡438处, 且主要以大型-特大型滑坡为主, 沿渭河及其支流岸坡密集分布(图 1), 本文选取其中317处无明显受阻的滑坡进行特征参数的幂律相依性探讨。
![]()
图 1 天水市麦积区幅滑坡分布图Figure 1. Distribution diagram of loess landslide in the Maiji district in the city of Tianshui1.2 研究方法
为研究区内黄土滑坡与其发生频率、规模参数和运动特征参数间的幂律相依性, 并建立经验关系式, 本文采用最小二乘法, 对区内滑坡特征参数进行幂函数拟合, 形式如下:
(1) 式中:NL--等于或者大于某一滑坡参数的累计频数;
AL--黄土滑坡的参数;
BL--滑坡规模参数;
CL--滑坡运动特征参数;
α1、α2、α3--幂指数;
C1、C2、C3--常数。
通过对式(1)两边取常用对数, 变为:
(2) 式(2)表明存在幂指数关系的参数, 在双对数坐标系下满足线性关系, 幂指数α1、α2、α3即为该直线的斜率, 其中D1、D2、D3为常数。
2. 黄土滑坡的幂律相依性
2.1 滑坡发生频率
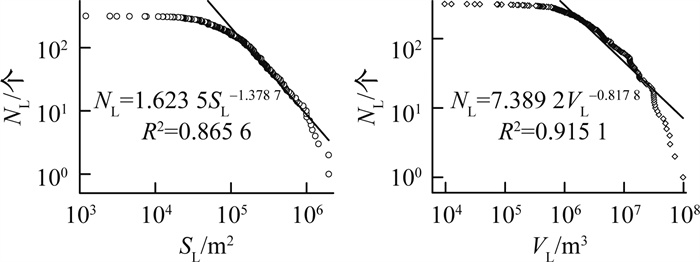
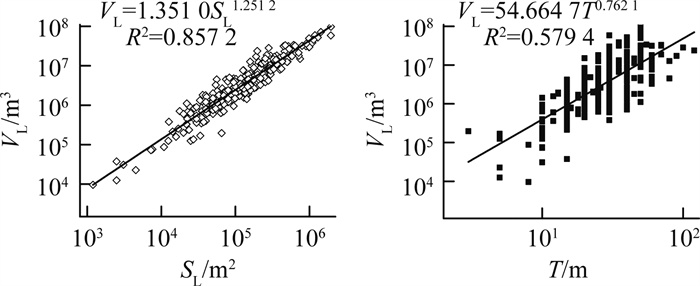
研究滑坡规模-累积频率的幂律相依性曲线, 可以得到滑坡发生大小与滑坡发生的概率性质[15]。麦积区幅内黄土滑坡面积SL-累积频率NL、体积VL-累积频率NL的拟合结果见图 2。
![]()
图 2 黄土滑坡面积(SL)、体积(VL)-累积频率(NL)的依存关系Figure 2. Power law relationships between area (SL), volume (VL) and cumulative frequency(NL) of loess landslides由图 2可知, 在一定范围内, 麦积区幅内黄土滑坡的累积频率的对数值分别随着面积和体积对数值的增大而减小, 呈负幂指数关系。值得注意的是, 当滑坡规模较小时, 滑坡发育的累积频率曲线并不沿着滑坡体积较大时的斜率呈线性增加, 而是发生了“偏转”。关于这一现象的形成原因, 有学者[16]认为, 规模小的滑坡因易遭后期改造, 在发生一段时间内不易辨别, 进而减少了小滑坡的统计个数;也有学者[17]认为, 形成这一现象主要受滑坡的组成物质、地形地貌等自然因素导致。分析认为, 研究区人类工程活动频繁, 该区域曲线发生“偏转”的主要原因是受人类工程活动影响, 小滑坡多被当地人类工程活动改造所致。研究区较大型滑坡的面积、体积与滑坡发生频率之间的经验关系式方程分别为:
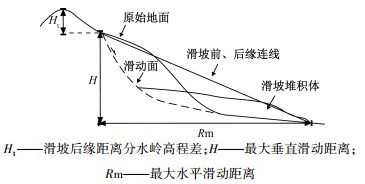
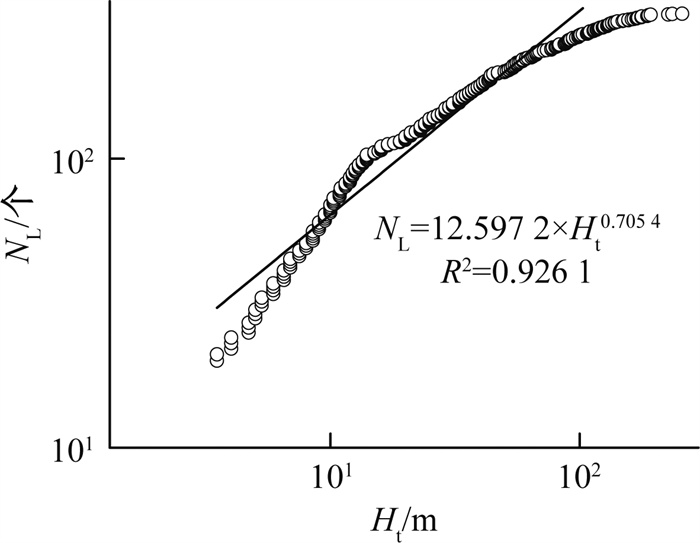
(3) (4) 研究发现, 黄土滑坡以及发生频率的幂律相依性不仅存在于滑坡面积与体积之间, 滑坡后缘距离分水岭高程Ht(图 3, 分水岭高程取滑坡滑向反向延长线上第一个分水岭高程)与其发生的频率NL之间也满足相依性原则, 其结果见图 4。
![]()
图 4 滑坡后缘距分水岭高程差(Ht)与累积频率(NL)之间的依存关系Figure 4. Power law relationships between the cumulative frequency(NL) and the height difference between loess landslide rear and watershed slopes(Ht)由图 4可知, 滑坡发生的累积频率的对数值随滑坡后缘距分水岭高程差对数值的增大而增大, 呈正幂函数关系, 且相关性好。二者的经验关系式表示为:
(5) 上述研究显示, 在一定范围内, 天水市麦积区幅内黄土滑坡以及发生频率之间的关系可以采用幂函数来表示, 其中, 面积-累积频率、体积-累积频率呈负相关关系, 滑坡后缘距离分水岭高程-累积频率呈正相关关系, 且它们的拟合效果都较好。表明滑坡-累积频率的幂律相依性不仅存在于滑坡面积-累积频率、体积-累积频率间, 还存在于滑坡后缘距离分水岭高程与其发生的累积频率之间。
2.2 滑坡发生规模
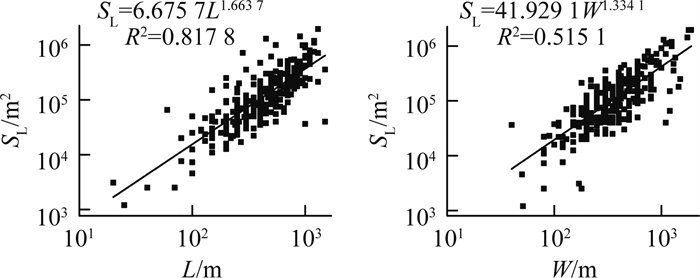
研究滑坡长、宽、厚度、面积、体积之间的幂律相依性, 就可以借助易测量的规模信息来推测那些不易测量的规模信息, 进而解决成百上千个滑坡体积难确定的难题。麦积区幅内黄土滑坡的体积与面积、体积与厚度、面积与长度以及面积与宽度之间的关系如图 5~6所示。
![]()
图 5 滑坡面积(SL)、厚度(T)与体积(VL)的依存关系Figure 5. Power law relationships betweenarea(SL), thickness(T) and volume(VL) of landslides![]()
图 6 滑坡长度(L)、宽度(W)与面积(SL)的依存关系Figure 6. Power law relationships between length(L), width(W) and area(SL) of landslides可以看出, 麦积区幅内黄土滑坡的体积的对数值随面积和厚度对数值的增大而增大, 面积的对数值又随滑坡的长度和宽度对数值的增大而增大, 且它们之间均呈现良好的正幂函数相关。其幂函数方程分别表示为:
(6) (7) (8) (9) 2.3 滑坡运动特征
本文所指滑坡运动特征参数包括滑坡的最大垂直滑动距离H(即滑坡前后缘高差)、最大水平滑动距离Rm(即滑坡前后缘距离)和滑坡前、后缘连线的斜率H/Rm(即滑坡的等效摩擦系数μ[18])(图 3)。
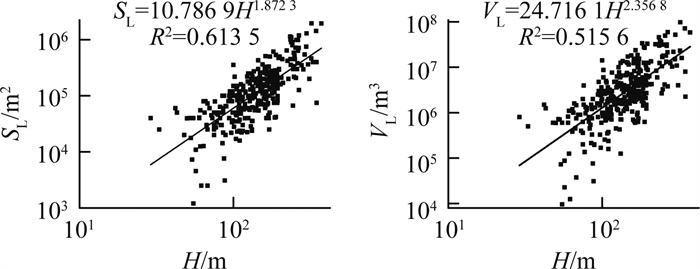
在双对数坐标系下, 研究区滑坡的最大垂直滑动距离与滑坡的发育面积、体积间的相互关系见图 7。
![]()
图 7 滑坡最大垂直滑动距离(H)与面积(SL)、体积(VL)的依存关系Figure 7. Power law relationships between area(SL), volume(VL) and maximum vertical sliding distance(H) of landslides由图 7可知, 滑坡面积、体积的对数值随着最大垂直滑动距离对数值的增大而增大, 它们之间呈正幂函数关系, 且相关性好。其经验关系式表示为:
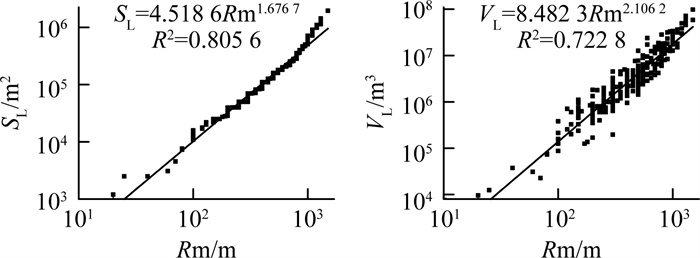
(10) (11) 同时, 在双对数坐标系下, 区内滑坡面积、体积与最大水平滑动距离间的相互关系见图 8。
![]()
图 8 滑坡最大水平滑动距离(Rm)与面积(SL)、体积(VL)的依存关系Figure 8. Power law relationships between area(SL), volume(VL) and maximum horizontal sliding distance(Rm) of landslides由图 8可知, 滑坡面积、体积的对数值也随滑坡最大水平滑动距离的对数值的增大而增大, 呈良好的正相关性。其经验关系式表示为:
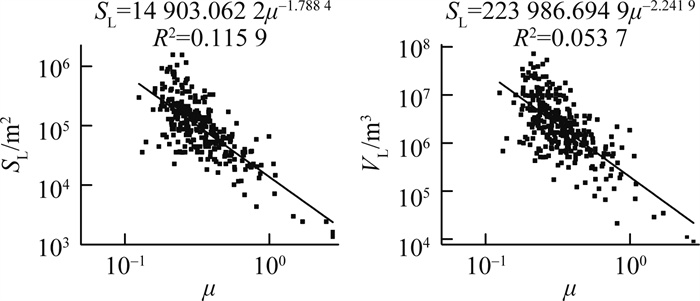
(12) (13) 此外, 在双对数坐标系下, 滑坡的等效摩擦系数(μ)与发育面积、体积间的相互关系如图 9所示。
![]()
图 9 滑坡的等效摩擦系数(μ)与面积(SL)、体积(VL)的依存关系Figure 9. Power law relationships between area(SL), volume(VL) and the sliding equivalent friction coefficient(μ) of landslides研究显示, 天水市麦积区幅内黄土滑坡的最大垂直滑动距离、最大水平滑动距离等运动特征参数与规模参数之间可以通过经验关系式来表示。它们之间通过幂函数拟合均呈现正相关性, 且拟合效果较好。这就可以在基于规模参数幂律相依性得知体积、面积的前提下, 估算滑坡运动的最大垂直距离和最大水平距离, 可以为滑坡运动特征研究提供一定参考。
需要说明的是, 滑坡的面积、体积的对数值随滑坡等效摩擦系数的对数值的增大而减小, 呈负相关性, 但相关性较差, 特别是等效摩擦系数与体积之间的相关性系数的二次方值极低。这说明, 上述建立的滑坡面积、体积与等效摩擦系数之间的经验关系式仅能代表其负相关的趋势, 进行定量研究还存在一定缺陷。究其原因, 主要是受以下几个方面影响:
(1)天水市麦积区幅内黄土滑坡的分布是历史地震滑坡和非地震滑坡的总和, 不同形成机理的滑坡其等效摩擦系数存在较大差异, 进而影响了其拟合效果;
(2)研究区滑坡多具有多期活动特点, 单个滑坡成因复杂是影响其拟合效果的重要因素;
(3)区内滑坡体部分受滑坡前缘冲沟阻挡, 致使野外调研得到的滑坡最大水平距离较真实的最大水平距离小, 导致等效摩擦系数与规模参数拟合存在误差。
2.4 黄土滑坡的幂律相依性对比分析
比较以往关于体积-累积频率、体积-面积的幂律相依性研究成果(表 1~2)可知:滑坡体积与累积频率幂函数关系的幂指数介于-0.072~-0.926之间, 平均值为-0.603 2;滑坡体积与面积幂函数关系的幂指数是介于0.88~1.95之间, 其平均值为1.253 5。天水市麦积区幅内黄土滑坡体积-累积频率、体积-面积关系的幂指数分别为-0.817 8和1.251 2, 均分布在-0.072~-0.926、0.88~1.95范围之内, 且体积-面积函数的幂指数接近于平均值1.253 5。表明区内黄土滑坡各参数的幂律相依性与以往研究成果存在着共同的趋势特征, 而天水市独特的黄土高原沟壑地貌, 特殊的滑坡组成物质-黄土, 使得其体积-面积函数的幂指数接近以往研究平均值, 这反映了这些经验关系式的幂指数可能与不同区域的环境地质条件紧密相关。
表 1 体积-累积频率经验关系式统计Table 1. Empirical relationship between the volume and the cumulative frequency
表 2 滑坡体积-面积经验关系式统计Table 2. Empirical relationship between volume and area
在滑坡及其发生频率的幂律关系中, 面积-累积频率关系式的幂指数为1.378 7, 体积-累积频率关系式的幂指数为0.817 8, 滑坡后缘距离分水岭高程-累积频率关系式的幂指数为0.705 4。这与国内外研究的滑坡面积-累积频率幂指数> 1、体积-累积频率幂指数< 1的趋势是相同的。幂指数的分布特征为面积-累积频率> 体积-累积频率> 滑坡后缘距离分水岭高程-累积频率。
在滑坡规模参数间的幂律关系中, 体积与面积关系式的幂指数为1.251 2, 体积与厚度关系式的幂指数为0.762 1, 面积与长度关系式的幂指数为1.663 7, 面积与宽度关系式的幂指数为1.334 1。幂指数的分布特征为面积与长度> 面积与宽度> 体积与面积> 体积与厚度。
在滑坡的运动特征参数间的幂律关系中, 滑坡面积、体积与滑坡的最大垂直滑动距离关系的相关性较好, 其幂指数分别为1.872 2,2.356 8;滑坡面积、体积与最大水平滑动距离关系的相关性也较好, 其幂指数分别为1.676 7,2.106 2;而滑坡面积、体积与滑坡的等效摩擦系数的相关性极差, 但它们之间呈负相关性的趋势应该是准确的。幂指数的分布特征为体积与最大垂直滑动距离> 体积与最大水平滑动距离> 面积与最大垂直滑动距离> 面积与最大水平滑动距离。
3. 结论
通过系统研究天水市麦积区内黄土滑坡的幂律相依性, 验证并拓宽了滑坡幂律规则的适用范围, 建立了特征参数之间依存关系的经验关系式。综合分析, 取得如下结论:
(1)滑坡-累积频率的幂律相依性不仅存在于滑坡面积-频率、体积-频率间, 还存在于滑坡后缘距离分水岭高程与发生的频率之间, 这为地质灾害调查和认识提供一定参考。
(2)黄土滑坡规模参数幂指数分布特征为面积与长度> 面积与宽度> 体积与面积> 体积与厚度;运动特征参数幂指数的分布特征为体积与最大垂直滑动距离> 体积与最大水平滑动距离> 面积与最大垂直滑动距离> 面积与最大水平滑动距离。
(3)滑坡的等效摩擦系数与滑坡面积、体积的幂函数相关性差, 故而该经验关系式仅能代表等效摩擦系数与滑坡面积、体积间的趋势特征, 不能作为定量分析的依据。
-
![]()
图 1 天水市麦积区幅滑坡分布图
Figure 1. Distribution diagram of loess landslide in the Maiji district in the city of Tianshui
![]()
图 2 黄土滑坡面积(SL)、体积(VL)-累积频率(NL)的依存关系
Figure 2. Power law relationships between area (SL), volume (VL) and cumulative frequency(NL) of loess landslides
![]()
图 4 滑坡后缘距分水岭高程差(Ht)与累积频率(NL)之间的依存关系
Figure 4. Power law relationships between the cumulative frequency(NL) and the height difference between loess landslide rear and watershed slopes(Ht)
![]()
图 5 滑坡面积(SL)、厚度(T)与体积(VL)的依存关系
Figure 5. Power law relationships betweenarea(SL), thickness(T) and volume(VL) of landslides
![]()
图 6 滑坡长度(L)、宽度(W)与面积(SL)的依存关系
Figure 6. Power law relationships between length(L), width(W) and area(SL) of landslides
![]()
图 7 滑坡最大垂直滑动距离(H)与面积(SL)、体积(VL)的依存关系
Figure 7. Power law relationships between area(SL), volume(VL) and maximum vertical sliding distance(H) of landslides
![]()
图 8 滑坡最大水平滑动距离(Rm)与面积(SL)、体积(VL)的依存关系
Figure 8. Power law relationships between area(SL), volume(VL) and maximum horizontal sliding distance(Rm) of landslides
![]()
图 9 滑坡的等效摩擦系数(μ)与面积(SL)、体积(VL)的依存关系
Figure 9. Power law relationships between area(SL), volume(VL) and the sliding equivalent friction coefficient(μ) of landslides
表 1 体积-累积频率经验关系式统计
Table 1 Empirical relationship between the volume and the cumulative frequency
下载: 导出CSV
-
[1] 杨立中, 王高峰, 王爱军, 等. 陇东黄土丘陵区滑坡形成机理分析--以环县西北地区为例[J]. 中国地质灾害与防治学报, 2016, 27(2): 39-48. YANG L Z, WANG G F, WANG A J, et al. Landslides mechanization in the loess hilly area of eastern Gansu province-case study in Huan county[J]. The Chinese Journal of Geological Hazard and Control, 2016, 27(2): 39-48. (in Chinese)
[2] 周飞, 许强, 巨袁臻, 等. 黑方台黄土斜坡变形破坏机理研究[J]. 水文地质工程地质, 2017, 44(1): 157-163. https://www.swdzgcdz.com/cn/article/id/201701024 ZHOU F, XU Q, JU Y Z, et al. A study of the deformation and failure mechanism of the Heifangtai loess slope[J]. Hydrogeology & Engineering Geology, 2017, 44(1): 157-163. (in Chinese) https://www.swdzgcdz.com/cn/article/id/201701024
[3] 王念秦. 黄土滑坡发育规律及其防治措施研究[D]. 成都: 成都理工大学, 2004. WANG N Q. Study on the growing laws and controlling measures for loess landslide[D]. Chengdu: Chengdu University of Technology, 2004. (in Chinese)
[4] 张茂省, 李同录. 黄土滑坡诱发因素及其形成机理研究[J]. 工程地质学报, 2011, 19(4): 530-540. DOI: 10.3969/j.issn.1004-9665.2011.04.014 ZHANG M S, LI T L. Triggering factors and forming mechanism of loess landslides[J]. Journal of Engineering Geology, 2011, 19(4): 530-540. (in Chinese) DOI: 10.3969/j.issn.1004-9665.2011.04.014
[5] 吴玮江, 王念秦. 甘肃滑坡灾害[M]. 兰州: 兰州大学出版社, 2006. WU W J, WANG N Q. Landslide hazards in Gansu[M]. Lanzhou: Lanzhou University Press, 2006. (in Chinese)
[6] 王念秦, 张倬元. 黄土滑坡灾害研究[M]. 兰州: 兰州大学出版社, 2005. WANG N Q, ZHANG Z Y. Study on loess landslide disasters[M]. Lanzhou: Lanzhou University Press, 2005. (in Chinese)
[7] 李媛, 吴奇. 孟家山黄土-红层接触面滑坡破坏机理研究[J]. 水文地质工程地质, 2001, 28(1): 52-54. DOI: 10.3969/j.issn.1000-3665.2001.01.015 LI Y, WU Q. Mengjiashan landslide causative mechanism along the contact between loess and Neocene red mudstone[J]. Hydrogeology & Engineering Geology, 2001, 28(1): 52-54. (in Chinese) DOI: 10.3969/j.issn.1000-3665.2001.01.015
[8] 田尤, 杨为民, 刘廷, 等. 天水锻压机床厂滑坡变形破坏机制及形成演化[J]. 地质力学学报, 2015, 21(2): 298-308. DOI: 10.3969/j.issn.1006-6616.2015.02.020 TIAN Y, YANG W M, LIU T, et al. Deformation mechanism and evolutionary process of Tianshui forging machine plant in Gansu[J]. Journal of Geomechanics, 2015, 21(2): 298-308. (in Chinese) DOI: 10.3969/j.issn.1006-6616.2015.02.020
[9] Per Bak, Chao Tang, Kurt Wiesenfeld. Self-organized Criticality: An Explanation of 1/f Noise[J]. Physical Review Letters, 1987, 59(4): 381-384. DOI: 10.1103/PhysRevLett.59.381
[10] 彭令, 徐素宁, 彭军还. 三峡库区滑坡规模与发育特征研究[J]. 现代地质, 2014, 28(5): 1077-1086. DOI: 10.3969/j.issn.1000-8527.2014.05.025 PENG L, XU S N, PENG J H. Research on Development Characteristics and Size of Landslides in the Three Gorges Area[J]. Geoscience, 2014, 28(5): 1077-1086. (in Chinese) DOI: 10.3969/j.issn.1000-8527.2014.05.025
[11] 许强, 黄润秋. 地质灾害发生频率的幂律规则[J]. 成都理工学院学报, 1997, 24(增刊1): 93-98. XU Q, HUANG R Q. Power law between volume and frequency of geological hazards[J]. Journal of Chengdu University of Technology, 1997, 24(Sup1): 93-98. (in Chinese)
[12] Dai F C, Lee C F. Frequency-volume relation and prediction of rainfall-induced landslide[J]. Engineering Geology, 2001, 59(3/4): 253-266. http://www.sciencedirect.com/science?_ob=ShoppingCartURL&_method=add&_eid=1-s2.0-S0013795200000776&originContentFamily=serial&_origin=article&_ts=1437958870&md5=9437676729eb094af86d5c55d2d515a7
[13] Fuyii Y. Frequency distribution of the magnitude of landslides caused by heavy rainfall[J]. Journal of the Seismological Society of Japan, 1969, 22: 244-247.
[14] 成玉祥, 张骏, 杜东菊. 天水地区新构造运动特征研究[J]. 工程地质学报, 2007, 15(4): 549-554. DOI: 10.3969/j.issn.1004-9665.2007.04.020 CHENG Y X, ZHANG J, DU D J. Study on neotectonic movement features in Tianshui area[J]. Journal of Engineering Geology, 2007, 15(4): 549-554. (in Chinese) DOI: 10.3969/j.issn.1004-9665.2007.04.020
[15] Guthrie R, Evans S. Magnitude and frequency of landslides triggered by a storm event, Loughborough Inlet, British Columbia[J]. Nature Hazards and Earth System Science, 2004, 4(3): 475-483. DOI: 10.5194/nhess-4-475-2004
[16] Guthrie R H, Evans S G. Analysis of landslide frequencies and characteristics in a natural system, coastal British Columbia[J]. Earth Surface Processes and landform, 2004, 29(11): 1321-1339. DOI: 10.1002/esp.1095
[17] Dahl M-P J, Mortensen L E, Jensen N H, et al. Magnitude-frequency characteristics and preparatory factors for spatial debris-slide distribution in the northern Faroe Islands[J]. Geomorphology, 2013, 188: 3-11. DOI: 10.1016/j.geomorph.2012.09.015
[18] Adrian E Schcidegger. On the prediction of the reach and velocity of catastrophic landslide[J]. Rock Mechanice, 1973, 5: 231-236. DOI: 10.1007/BF01301796
[19] Hungr O, Evans S, Hazzard J. Magnitude and frequency of rock falls and rock slides along the main transportation corridors of southwestern British Colunbia[J]. Canadian Geotechnical Journal, 1999, 36(2): 224-238. DOI: 10.1139/t98-106
[20] Dussauge Peisser C, Helmstetter A, Grasso J R, et al. Probabilistic approach to rock fall hazard assessment: potential of historical data analysis[J]. Natural Hazards and Earth System Science, 2002, 2(1/2): 15-26. DOI: 10.5194/nhess-2-15-2002
[21] ten Brink U S, Geist E L, Andrews B D. Size distribution of submarine landslides and its implication to tsunami hazard in Puerto Rico[J]. Geophysical Research Letters, 2006, 33(11): L11307. DOI: 10.1029/2006GL026125/pdf
[22] Chaytor J D, Ten Brink U S, Solow A R, et al. Size distribution of submarine landslides along the US Atlantic margin[J]. Marine Geology, 2009, 264: 16-27. DOI: 10.1016/j.margeo.2008.08.007
[23] Guzzetti F, Ardizzone F, Cardinali M, et al. Distribution of landslides in the Upper Tiber River basin, central Italy[J]. Geomorphology, 2008, 96(1): 105-122. http://geomorphology.irpi.cnr.it/Geomorphology/publications/repository/public/abstracts/2007/DistributionLandslidesUTRB_EGU2007-J-02685.pdf
[24] Simonett D S. Landslide distribution and earthquakes in the Bewani and Torricelli Mountains, New Guinea[C]//Landform Studies from Australia and New Guinea. Cambridge: Cambridge University Press, 1967: 64-84.
[25] Rice R M, Foggin Ⅲ G T. Effects of high intensity storms on soil slippage on mountainous watersheds in Southern California[J]. Water Resources Research, 1971, 7(6): 1485-1496. DOI: 10.1029/WR007i006p01485
[26] Abele G. Bergsturze in den Alpen-IhreVerbreitung, Morphologie und Folgeerscheinungen[J]. Wissenschaftliche Alpenvereinshefte, 1974, 25: 247.
[27] Larsen M C, Torres Sanchez A J. The frequency and distribution of recent landslides in three montane tropical regions of Puerto Rico[J]. Geomorphology. 1998, 24(4): 309-331. DOI: 10.1016/S0169-555X(98)00023-3
[28] Martin Y, Rood K, Schwab J W, et al. Sediment transfer by shallow landsliding in the Queen Charlotte Islands, British Columbia[J]. Canadian Journal of Earth Sciences, 2002, 39(2): 189-205. DOI: 10.1139/e01-068
[29] 邱海军, 曹明明, 王雁林, 等. 黄土丘陵区地质灾害规模参数幂律相依性研究[J]. 地理科学, 2015, 35(1): 107-113. QIU H J, CAO M M, WANG Y L, et al. Power law correlations of geohazards in loess hilly region[J]. Scientia Geographica Sinica, 2015, 35(1): 107-113. (in Chinese)
[30] Korup O. Geomorphic imprint of landslides on alpine river systems, southwest New Zealand[J]. Earth Surface Processes and Landforms, 2005, 30(7): 783-800. DOI: 10.1002/esp.1171
-
期刊类型引用(1)
1. 方汕澳，许强，修德皓，赵宽耀，李志刚，蒲枫. 基于斜率模型的突发型黄土滑坡失稳时间预测. 水文地质工程地质. 2021(04): 169-179 . 
本站查看
其他类型引用(5)
计量
- 文章访问数: 1099
- HTML全文浏览量: 91
- PDF下载量: 838
- 被引次数: 6
邮件订阅
RSS