地下水是可供人类利用的重要资源, 而随着社会经济持续发展和人口快速增长, 工业污水排放、化肥农药施用、垃圾填埋等导致了大量污染物进入地下水, 地下水污染现已成为全世界共同关注的问题之一。持续泄露的可溶性污染物在地下水流运动的长期作用下可运移数公里甚至数百公里远, 严重影响了地下水环境。研究治理地下水污染, 首先要了解此类污染的过程和特征, 对其运移过程中水流场和浓度场变化的研究也十分关键^[1]。孙家强等^[2]以黏土模拟低渗透包气带环境, 探究了混溶流体在包气带中的迁移规律; 左自波等^[3]模拟了土体非饱和带中污染物在降雨条件下的迁移过程; 余期冲等^[4]研究了死端孔隙对溶质运移的影响。但以上研究中对于孔隙微观结构影响的探讨不多。

黏土多孔介质结构十分复杂, 并影响着土体的宏观特征(孔隙度、毛细压力、相对渗透率等), 进而影响了溶质的运移。对于黏土微观孔隙结构研究的主要问题在于多孔介质的描述问题, 即如何采用数学的方法对微观孔隙结构进行定量描述。大多传统研究中采用只能反映“整体”性能的连续介质模型, 故不能反映其微观特征^[5]。对于微观研究, 首先需构建多孔介质的微观结构, Tacher L等^[6]采用一种离散的减少距离的方法生成圆形、椭圆形的两相粒状多孔介质; Pilotti等^[7]采用球体沉降法生成三维多孔介质; 这两类方法生成的孔隙结构比较简单, 虽然也能反映一定的特征, 但是和实际形态仍有差距。Dong Hu等^[8]、刘向君等^[9]、黄家国等^[10]等学者采用扫描成像技术分析微观孔隙结构, 但成本高昂。Wang M等^[11]结合多孔介质构造的孔隙生长模型和丛生理论, 提出了四参数随机生长方法(Quartet Structure Generation Set, QSGS); 周潇等^[12]利用该方法探讨了渗流速度与孔隙通道大小和土颗粒大小之间的关系。与传统的圆形(或椭圆形)颗粒构造的黏土微观结构相比, 使用随机生长四参数生成法构造的黏土微观结构与真实情况更接近。

黏土多孔介质内部通道形态各异, 且分布不规律, 在渗流过程中常出现一些沿着优先途径的集中流动, 统称为优先流^[13]。本文利用随机生长四参数法构建多孔介质模型, 通过Stokes Equation (Stokes方程) 与Advection-Diffusion Equation (对流扩散方程, ADE) 的耦合计算, 模拟黏土多孔介质中可溶性污染物的运移过程, 旨在探讨黏土微观结构对可溶性污染物运移的影响。

1.   控制方程及问题的建立

1.1   黏土微观孔隙结构的生成

为获得黏土多孔介质的微观孔隙结构, 采用了随机生长四参数生成法(QSGS)生成多孔介质的孔隙轮廓, 并用AutoCAD建立可供有限元分析软件使用的模型。该方法的构造过程接近于多孔介质的生成过程, 与传统的圆形或椭圆形颗粒构成的多孔介质相比, 其固相颗粒形态不规则且大小具有随机性, 生成的多孔介质孔隙包含连通孔隙和非连通孔隙。模型的构建主要步骤如下:

(1) 利用Matlab实现Wang M等^[11]提出的随机生长四参数生成法的程序编译, 生成孔隙度n为0.7的多孔介质轮廓, 保存固相颗粒的轮廓坐标数据:

① 确定一定大小的构造区域(本文采用199×199的节点范围), 初始状态该范围内全为孔隙。随机分布初始固体颗粒, 分布概率P_a应小于最终多孔介质固相所占比例。游历构造区域内的每个节点并在[0, 1]内取随机数, 随机数小于或等于P_a的节点设置为初始固体颗粒。

② 在初始固体颗粒位置按不同方向的生长概率P_i生成固相颗粒: 取8个生长方向(i=1, 2, …, 8), 其中包括4个主要生长方向(i=1, 2, 3, 4)和4个次生长方向(i=5, 6, 7, 8), 生长概率不都相同且P_1~4> P_5~8, 本文中P_1~4=0.1、P_5~8=0.025, 可获得各向异性的多孔介质。各方向相邻节点在[0, 1]内取随机数, 随机数小于或等于P_i的节点生长为固体颗粒。

③ 反复执行步骤②, 直至孔隙率达到设定值n。生成固相颗粒轮廓图并保存轮廓坐标数据。

(2) 运行AutoCAD中的VBA宏程序, 将固相颗粒的轮廓坐标数据自动绘制成大小为19.9 mm×19.9 mm的轮廓模型, 并添加四周边界后, 保存为可供有限元分析软件COMSOL使用的DXF文件。

(3) 将所得的DXF文件导入COMSOL, 模型不同区域设置为固相材料或液相材料。

1.2   控制方程

微观结构黏土的可溶性污染物运移问题是水流场和浓度场的两场耦合问题, 因此, 分别对水流场和浓度场的控制方程进行阐述。为了更真实地模拟黏土微观结构中水流场的状态, 采用Stokes方程:

式中: ρ——水密度/(kg·m^-3);

g——重力加速度/(m·s^-2);

φ——水头高度/m;

μ——水的动力黏滞系数/(kg·m^-1·s^-1);

u——水流速度矢量/(m·s^-1)。

通过上式, 可解出黏土多孔介质中的非均匀速度场, 将非均匀速度场代入对流-扩散方程:

式中: u——由式(1)计算得到的二维水流场速度矢量;

c——可溶性污染物的浓度/(mol·L^-3);

D_f——分子扩散系数/(m²·s^-1)。

本文假设D_f=1.0×10^-9 m²/s。需要注意的是, 式(3)表示本文考虑的可溶性污染物具有理想特征, 即不考虑污染物的化学反应特征, 且在颗粒表面无吸附。

1.3   问题的建立和求解

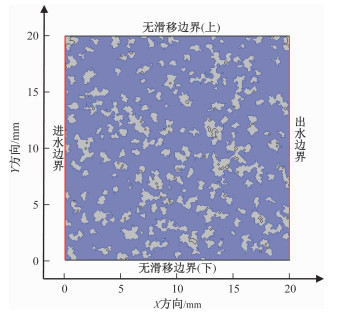
本文旨在利用数值模拟的方法探讨各向异性黏土多孔介质对可溶性污染物运移的影响。使用上述DXF格式的图像文件在COMSOL中建立孔隙度n为0.7的多孔介质几何模型(图 1)。其水流场设置为: 左边和右边的进口和出口边界为定压力边界, 颗粒边界和上下边界为无滑移边界, 水流在5 Pa的压力下流动。

图  1  孔隙度n=0.7的多孔介质模型

Figure  1.  Porous media model (n=0.7)

下载: 全尺寸图片 幻灯片

COMSOL是一款基于多物理场耦合的有限元计算分析软件, 可以用来求解线性、非线性问题及与时间有关的稳态、瞬态问题。本文通过Stokes Equation (Stokes方程) 与Advection-Diffusion Equation (对流扩散方程, ADE) 的耦合, 利用有限元的方法对计算区域进行网格剖分细化、求解, 输出速度场和随时间变化的浓度场数据及图形。

2.   黏土微观结构中水流场分析

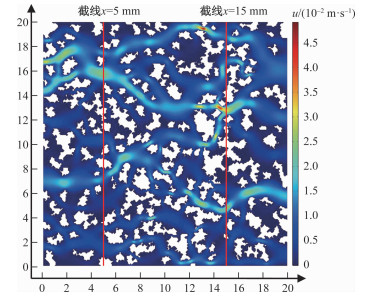
黏土微观结构中的水流场是研究可溶性污染物运移的基础。水流场的控制方程由式(1)和式(2)构成。为真实反映多孔介质地下水水流状态, 由进口和出口5 Pa压力差控制的平均水流场速度为0.005 m/s, 相应的水流场分布如图 2所示。

图  2  水流场分布(单位：m·s^-1)

Figure  2.  Flow field distribution (unit: m·s^-1)

下载: 全尺寸图片 幻灯片

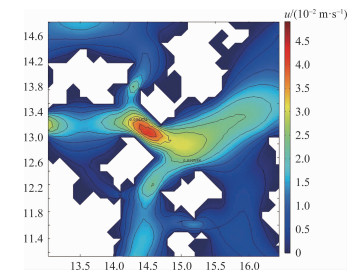
图 3显示了孔隙度n=0.7的黏土微观孔隙通道中在5 Pa的压力下水流场的分布情况。其分布十分复杂, 受孔隙连通情况、孔隙形态、颗粒分布和大小的影响明显, 最快流速达到0.0478 m/s, 而最慢流速接近于0。从图 3选取的微观孔隙通道的流速等值线图可以发现, 孔隙中的流速基本满足速度由中心区域向四周降低的特征。而此通道隙宽较窄且连通性好, 共与四个有水流流动的通道相连接, 出现了流速峰值。

图  3  微观孔隙通道内水流场分布(单位：m·s^-1)

Figure  3.  Distribution of water flow in micro-pore channel (unit: m·s^-1)

下载: 全尺寸图片 幻灯片

计算区域存在类似于土体渗流中沿着优先途径集中流动的优先流现象, 优先流与水流方向大致平行。几条高速流在某些通道处汇聚成更大的优先流, 又在某些通道处分散开, 导致了水流场分布的不均匀性, 而这种优先流分布具有随机性。

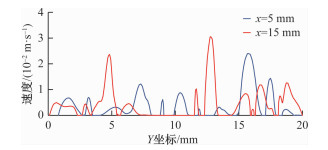
为研究孔隙内流速分布特征, 选取x=5 mm和x=15 mm两个剖面上孔隙流速。由图 4可知, 接近颗粒边界的节点速度几乎为零, 这是由于将颗粒表面设置成无滑移边界条件。每条截面上均有多个速度峰值, 结合速度曲线和截线上孔隙通道特征, 我们发现速度峰值往往出现在孔隙连通情况较好的位置, 如x=15 mm剖面上的最大速度其所在孔隙位置上四个方向上均有水流流动, 并且孔隙通道隙宽较小; 而低速区域一般孔隙连通情况差或位于死端孔隙。正是因为介质中颗粒和孔隙分布的随机性, 造成水流速度分布的差异而导致了污染物运移在介质中的各向异性。

图  4  剖面上水流分布

Figure  4.  The distribution of water on the profile

下载: 全尺寸图片 幻灯片

用相同的方法构建孔隙度n=0.6的黏土多孔介质模型, 分别对不同孔隙度模型的两个截面上的流速做均匀性分析。本文采用相对标准偏差CV(CV值与速度均匀性呈负相关)、均匀性指数γ_v和克里斯琴森均匀系数CU三个指标进行评价^[14]。

表  1  截面速度均匀性指数

Table  1.  Velocity uniformity index

下载: 导出CSV 

| 显示表格

通过对比以上三个指标可发现, 其中两模型不同位置的CV值均超过了1, 这表明剖面速度分布十分不均匀; 同时两剖面位置的γ_v较小, CU接近于0, 结果也表明了均匀性差的特征; 而孔隙度变化对水流场均匀性的影响不明显。我们认为这是剖面上孔隙和颗粒的随机分布所导致的结果, 即多孔介质颗粒形态、分布情况和孔隙连通性、大小共同影响了水流场分布特征。

3.   可溶性污染物的浓度场穿透曲线分析

为了更真实地反应可溶性染污物在黏土微观结构中地下水流作用下污染和运移的过程, 本文采用脉冲式注入可溶性污染物, 浓度C₀=1 mol/L。计算总时长为30 s, 其中0~10 s为可溶性污染物从左边进口边界注入时段, 随后左边进口边界改注纯水。

3.1   初始水头压力对可溶性污染物运移过程的影响分析

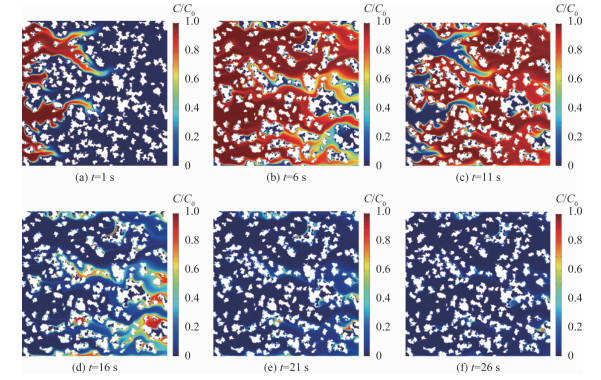
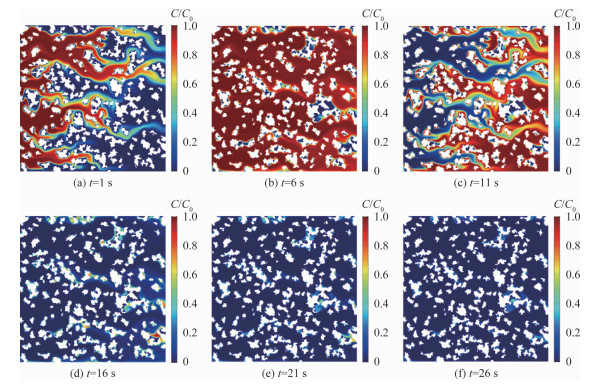
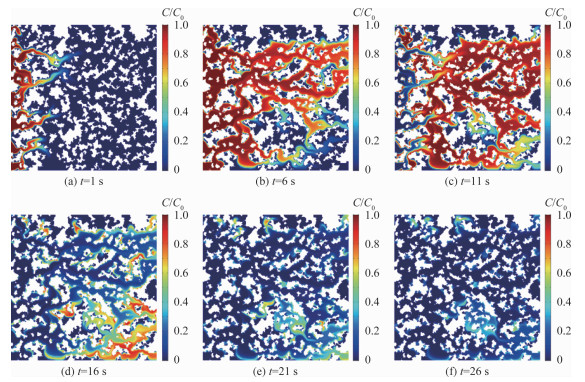
为了探究不同水头压力条件下可溶性污染物溶质运移的情况, 将初始压力分别设置为5 Pa和10 Pa, 在其他条件不变的情况下, 进行计算模拟。图 5~6分别显示了可溶性污染物在初始压力在P=5 Pa和10 Pa下的运移过程。

图  5  当水头压力为5 Pa时污染物运移过程(n=0.7)

Figure  5.  Contaminant transport process (5 Pa, n=0.7)

下载: 全尺寸图片 幻灯片

图  6  当水头压力为10 Pa时污染物运移过程(n=0.7)

Figure  6.  Contaminant transport process (10 Pa, n=0.7)

下载: 全尺寸图片 幻灯片

通过对比分析可以看出孔隙的分布、颗粒形状以及孔隙度对于可溶性污染物的运移情况有较大影响。可溶性污染物扩散是一个首先占据大孔隙通道, 然后向狭小孔隙扩散的过程: 大孔隙通道内水流流速快、流通性好, 注入的可溶性污染物在高速水流作用下充满这类孔隙通道; 而大孔隙通道周边狭小孔隙中的水流流速小, 对流作用不明显, 污染物在分子扩散作用下向小孔隙内缓慢迁移。在同样的时间内, 高压力条件下污染物能够扩散得更远, 且侵入微小孔隙的能力更强。

同时, 其扩散与水流流速也有关联, 在颗粒表面水流速度较小处, 可溶性污染物侵入颗粒表面的能力远远小于其在水流方向上的运移能力。污染物前缘锋面的运动方向与孔隙形态、分布有很大关联, 锋面总体上沿着水流方向在连通较好的孔隙中移动, 且污染物的运移主方向与水流的优势流方向一致。

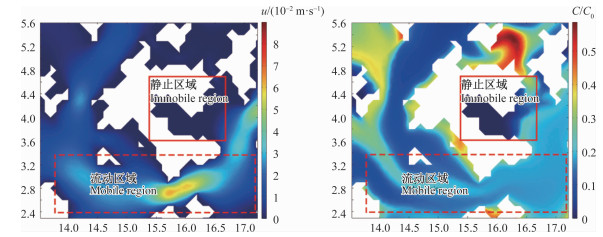
在运移过程中, 可以发现一些区域的浓度变化滞后于浓度中心的运移: 在注入可溶性污染物一段时间后, 大部分研究区域为高浓度的污染物, 但也有零星分布的区域内污染物浓度较低或为零; 而改注纯水后, 当大部分研究区域浓度降为零时这些区域污染物浓度仍然较高。这是由于在流动区域存在可流动区域(Mobile region)和静止区域(Immobile region), 静止区往往是一些微小空隙或死端孔隙。如图 7所示, 在静止区域内水流几乎不流动, 主要是在分子扩散作用主导下的溶质运移过程, 因此, 在运移过程后期静止区域仍残留高浓度的污染物。此类污染会在黏土介质中残留很长时间, 且不会随着水流的流动而消失。

图  7  不同流动区域水流场及浓度场分布

Figure  7.  Flow field and concentration field distribution in different flow areas

下载: 全尺寸图片 幻灯片

3.2   孔隙度对可溶性污染物运移过程的影响分析

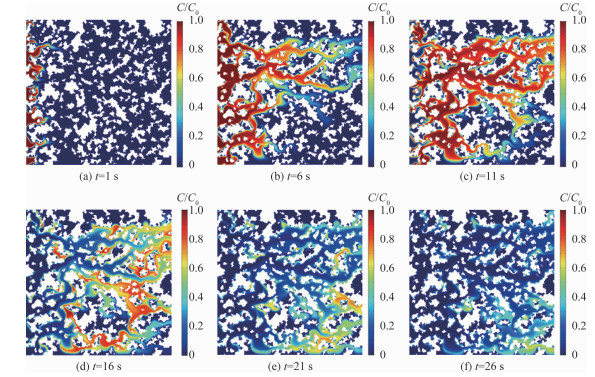
使用同样的方法构建n=0.6的黏土多孔介质模型, 在其他条件不变的情况下进行模拟计算。为保证注入的污染物基本穿过右出口界面, 将计算总时长延长至50 s, 污染物注入时长不变。对比发现, 初始压力差异的影响与孔隙度n=0.7的模型表现一致, 体现了水流场对于污染物迁移的作用。

通过对比相同压力条件下不同孔隙度模型中的污染物运移过程, 可以发现污染物前缘也沿着水流优势流方向移动, 而可溶性污染物沿着大孔隙通道运移的过程更突出。当污染物抵达右边界时, 与孔隙度n=0.7的模型内浓度场情况不同, 仍有较多区域保持低浓度状态, 小孔隙度介质中不同空隙区域的浓度差异更明显, 污染物扩散至这些区域需要更长的时间, 滞后现象更明显。对于孔隙度大的介质模型, 污染物前缘锋面抵达右边界耗时短, 污染物更容易充满整个介质。

图  8  当水头压力为5 Pa时污染物运移过程(n=0.6)

Figure  8.  Contaminant transport process (5 Pa, n=0.6)

下载: 全尺寸图片 幻灯片

图  9  当水头压力为10 Pa时污染物运移过程(n=0.6)

Figure  9.  Contaminant transport process (10 Pa, n=0.6)

下载: 全尺寸图片 幻灯片

3.3   穿透曲线分析

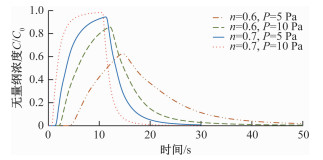
图 10显示了在不同压力边界条件, 黏土微观结构中可溶性污染物运移的穿透曲线。在本文中, 对于不同孔隙度模型下不同初始压力的算例, 穿透曲线的计算位置均选择在多孔介质模型右出水口处。在COMSOL中输出时长为50 s(步长0.05 s)的无量纲浓度变化情况, 并以时间为横坐标绘制穿透曲线, 其中无量纲浓度的表达式为:

图  10  不同初始压力下黏土微观结构中可溶性污染物运移穿透曲线

Figure  10.  Breakthrough curves of transport of soluble contaminants under different initial pressures

下载: 全尺寸图片 幻灯片

式中: L_y——出口边界y方向的长度/m;

u——由式(1)计算得到的出口边界水流速度/(m·s^-1);

C——可溶性污染物的浓度/(mol·L^-3);

C₀——污染物初始浓度/(mol·L^-3)。

四条曲线反映出污染物的到达时间存在明显的先后差异, 曲线峰值依次右移且不断降低, 穿透曲线的斜率逐渐减小。对比不同孔隙度的穿透曲线, 我们发现随着孔隙度降低穿透曲线峰值随时间轴向右移动且降低, 达到峰值后下降速度减缓, 这表明污染物在小孔隙度介质中迁移得更慢且同时间内残留污染物更多; 在同孔隙度中高初始压力条件下穿透曲线的斜率更大更陡峭, 在达到峰值后下降更快, 这是由于对流作用是影响污染物运移的主要因素, 在更大的初始压力作用下, 水流速度更快。可以发现当初始压力更大时, 穿透曲线的峰值浓度更接近于1, 也表明了相对于低压力情况下运移后期在微观结构中残留的污染物较少, 这一点通过对比图 5(f)和图 6(f)的运移图像也能说明。

同时, 所得的穿透曲线呈现不对称分布, 污染物的流出存在滞后效应, 即在曲线达到峰值后污染物浓度的下降趋势小于达到前的上升趋势且时间变长, 不同情况下曲线均表现出一定拖尾现象, 在低压力、小孔隙度条件下表现最明显。本文中没有考虑溶质化学反应和吸附现象, 造成该现象的原因我们认为是介质孔隙形态、颗粒的不均匀分布造成的; 孔隙大小和随机分布情况影响着在该孔隙内水流场的分布和浓度场的变化, 狭小孔隙和连通性较差的孔隙通道往往在运移过程后期仍残留较大浓度的污染物, 此类孔隙越多, 一定时间内则残留的污染物越多且水流带出污染物的效果越缓慢, 使得穿透曲线的拖尾现象越明显。

4.   结论

(1) 由于黏土微观结构中颗粒与孔隙分布具有随机性, 颗粒表面形状复杂, 其水流场分布具有很强的随机性, 水流流速分布十分不均匀。

(2) 水流场中存在的优先流现象, 与孔隙大小及其连通情况密切相关, 速度峰值往往出现在连通性较好且孔隙宽度较窄的位置。

(3) 可溶性污染物的运移过程与水流场密切相关, 水流场中的静止区域由于水流几乎不流动而受分子扩散作用主导, 往往容易残留高浓度污染物, 是污染后期的主要污染残留位置。

(4) 微观结构中的孔隙随机分布(如一些微小空隙或死端孔隙)是穿透曲线出现“托尾”现象的主要原因, 其“托尾”现象随初始压力的增大而减弱。