Evaluation and modification of the Lucas-Washburn model during capillary water rising in the layered soil
-
摘要:
受界面效应影响,毛细水在层状土中运移规律还难以用描述均质土中水分运移规律的Lucas-Washburn(LW)渗吸模型进行描述。基于此,本文设计了层状土室内模型试验,采用分布式的主动加热光纤法(简称AHFO)监测毛细水上升过程。根据AHFO测试结果,进一步对LW模型进行了修正,提出了适用于描述层状土中毛细水上升规律的ILW模型,并对ILW模型进行了试验验证。试验结果表明:(1)当毛细水湿润锋抵达“黏土(下部)-砂土(上部)”界面时,会产生“毛细屏障作用”,从而导致上部砂土中毛细水含水率急剧下降;(2)“毛细屏障作用”由砂土和黏土中的基质吸力不均衡造成,基质吸力大小由含水率决定;(3)当毛细水湿润锋抵达“砂土(下部)-黏土(上部)”界面时,在界面处出现“反毛细屏障作用”,从而导致上部黏土层中的含水率比相邻下部砂土层含水率更高;(4)虽然常见的LW模型可准确预测均质土中毛细水上升高度及速率,但受“毛细屏障作用”和“反毛细屏障作用”影响,LW模型在层状土中失效;(5)相比LW模型,ILW模型精度更高,能够更加准确地描述层状土中毛细水上升规律。
-
关键词:
- 层状土 /
- 主动加热光纤法(AHFO) /
- 毛细水 /
- Lucas-Washburn渗吸模型
Abstract:In the layered soils, the common Lucas-Washburn (LW) model that describes water movement in homogeneous soil always loses effectiveness under the influence of interfaces between adjacent layers. To characterize vertical water rise under capillary force, a laboratory model test was performed, in which soil moisture content profiles were monitored using the actively heated fiber optic method (AHFO). Based on the results obtained using the AHFO method, the LW model was revised, and an improved LW model (ILW) model was proposed. The experimental results show that (1) when the capillary water wetting front arrives at a "lower clay-upper sand interface", a "capillary barrier " can obviously be observed, which makes the soil moisture content above the interface much less than that in the lower soil; (2) the "capillary barrier effect" is caused by the unbalanced matrix suction between sand and clay; (3) while the capillary water wetting front reaches a "lower sand-upper clay" interface, the "anti-capillary barrier effect" around the middle interface appears, which leads to the soil moisture of the upper clay much larger than that of the lower sand; (4) the LW model becomes inaccurate due to the impacts of the "capillary barrier action" and "anti-capillary barrier action", and (5) compared with the LW model, the ILW model has higher accuracy in the layered soils.
-
受淋溶-淀积、剥蚀-沉积、生物扰动等作用, 层状结构土壤在自然界广泛分布[1]。层状土中水力特性的不连续, 导致其水分运移和赋存特征与均质土壤中的情况完全不同。在毛细水上升过程中, 土壤中的分层结构可能会阻碍(或加速)水分垂直方向的运动[2~4]。有关层状土中界面效应对水分运移规律影响的研究成果已较多。Hill等[5]发现土壤层状结构对水分入渗起抑制减渗作用。Baker等[6]指出水分在穿越细砂-粗砂的界面时会出现滞留。付志文等[7]将毛细水运移过程分为四个阶段, 即惯性力作用阶段, 黏性力-惯性力作用阶段, 黏性力作用阶段和黏性力-重力作用阶段。Zettl等[8]比较了加拿大阿尔伯达省油砂地区田间深1 m的土壤剖面持水量, 结果表明具有分层结构的土壤田间持水量高于均匀土壤, 并有利于作物高产。因此, 建立层状土中描述毛细水上升规律的模型非常重要。
目前描述毛细水运移最常用的渗吸模型有: Lucas-Washburn模型、Terzaghi模型、Handy模型、Bosanquet模型和纯惯性力模型等[9~12]。19世纪初, Lucas等[13]分析了等截面毛细管和多孔材料界面中水分自吸的作用因素, 并提出了经典的Lucas-Washburn(LW)模型。后来很多关于自吸的理论分析和实验研究大多数在LW模型的基础上进行。蔡建超等[1]综述了常用的自发渗吸理论模型, 总结了近十年来自发渗吸理论的研究进展和现状, 分析了渗吸机理判别参数, 简述了数值模拟研究及渗吸率影响机理的实验研究现状; Cai等[14]基于弯曲流线的分形特征, 通过引入弯曲毛细管的弯曲度和分形维数, 获得毛细管上升的高度/重量随时间演变的解析表达式。然而, 目前大部分模型都是用于描述均质土中毛细水上升, 关于层状土的研究还很少, 主要原因是受测试技术的限制, 层状土界面影响很难实际测定, 从而难以进一步验证相关模型。
目前, 对于毛细水运移与赋存特征的测试方法都是点式的, 如取样烘干法、干湿计法和时域反射法, 这些方法对均质土含水率的测试效果较好, 但是空间分辨率低, 难以更加精确测定层状土中水分信息; 遥测法、地面热辐射测量法、卫星遥感法等测量精度较低, 主要用于测量地表土层含水率[15~16]。而近几年发展起来的主动加热光纤法(Actively heated fiber optic method, AHFO)具有测试精度高、速度快、操作简便、可以连续分布式实时监测土中水分场等优势, 曹鼎峰等[17]、严珺凡等[18]已对AHFO法测试水分场的可行性进行了验证。
本文将基于AHFO测试结果对LW模型进行评价, 进一步对其进行改进, 并通过室内试验测定改进前后LW模型的精度。
受淋溶-淀积、剥蚀-沉积、生物扰动等作用, 层状结构土壤在自然界广泛分布[1]。层状土中水力特性的不连续, 导致其水分运移和赋存特征与均质土壤中的情况完全不同。在毛细水上升过程中, 土壤中的分层结构可能会阻碍(或加速)水分垂直方向的运动[2~4]。有关层状土中界面效应对水分运移规律影响的研究成果已较多。Hill等[5]发现土壤层状结构对水分入渗起抑制减渗作用。Baker等[6]指出水分在穿越细砂-粗砂的界面时会出现滞留。付志文等[7]将毛细水运移过程分为四个阶段, 即惯性力作用阶段, 黏性力-惯性力作用阶段, 黏性力作用阶段和黏性力-重力作用阶段。Zettl等[8]比较了加拿大阿尔伯达省油砂地区田间深1 m的土壤剖面持水量, 结果表明具有分层结构的土壤田间持水量高于均匀土壤, 并有利于作物高产。因此, 建立层状土中描述毛细水上升规律的模型非常重要。
目前描述毛细水运移最常用的渗吸模型有: Lucas-Washburn模型、Terzaghi模型、Handy模型、Bosanquet模型和纯惯性力模型等[9~12]。19世纪初, Lucas等[13]分析了等截面毛细管和多孔材料界面中水分自吸的作用因素, 并提出了经典的Lucas-Washburn(LW)模型。后来很多关于自吸的理论分析和实验研究大多数在LW模型的基础上进行。蔡建超等[1]综述了常用的自发渗吸理论模型, 总结了近十年来自发渗吸理论的研究进展和现状, 分析了渗吸机理判别参数, 简述了数值模拟研究及渗吸率影响机理的实验研究现状; Cai等[14]基于弯曲流线的分形特征, 通过引入弯曲毛细管的弯曲度和分形维数, 获得毛细管上升的高度/重量随时间演变的解析表达式。然而, 目前大部分模型都是用于描述均质土中毛细水上升, 关于层状土的研究还很少, 主要原因是受测试技术的限制, 层状土界面影响很难实际测定, 从而难以进一步验证相关模型。
目前, 对于毛细水运移与赋存特征的测试方法都是点式的, 如取样烘干法、干湿计法和时域反射法, 这些方法对均质土含水率的测试效果较好, 但是空间分辨率低, 难以更加精确测定层状土中水分信息; 遥测法、地面热辐射测量法、卫星遥感法等测量精度较低, 主要用于测量地表土层含水率[15~16]。而近几年发展起来的主动加热光纤法(Actively heated fiber optic method, AHFO)具有测试精度高、速度快、操作简便、可以连续分布式实时监测土中水分场等优势, 曹鼎峰等[17]、严珺凡等[18]已对AHFO法测试水分场的可行性进行了验证。
本文将基于AHFO测试结果对LW模型进行评价, 进一步对其进行改进, 并通过室内试验测定改进前后LW模型的精度。
1. 毛细水运移与赋存原理
1. 毛细水运移与赋存原理
1.1 Lucas-Washburn(LW)渗吸模型
毛细水主要受到基质吸力Fcap、毛细管侧壁的黏性阻力Fvisco和毛细水自身重力Fgrav作用。毛细水上升过程中液体充分发展的稳态阶段在整个上升过程中占有重要地位, 此时的流体可视为层流, 尤其是通过一个等截面圆管的流体流动被认为是Hagen-Poiseuille流动[19], 其流动的控制方程可直接由纳维-斯托克斯方程(Navier-Stokes)[20]求得。根据计算有:
(1) 式中: γ——毛细水液面张力;
φ——接触角;
R——平均空隙半径;
η——流体黏度;
ρ——毛细水密度;
g——重力加速度;
t——时间;
h——毛细水上升高度。
在黏性力作用阶段, Lucas和Wash burn忽略式(1)中惯性力和重力的作用, 提出了该阶段的简化模型(LW):
(2) 对于黏性力-重力作用阶段, Washburn在考虑了毛细水重力、黏性阻力和基质吸力作用, 求解出式(1)的隐形解:
(3) 式中,
当基质吸力和毛细水重力相平衡时, 毛细水上升到最大高度, 可以求得最大高度heq为:
(4) 毛细水达到最大高度后, 其运移过程趋于平衡, 此时其表现出的特征称为毛细水赋存特征, 常用土壤水分特征曲线表征。
1.1 Lucas-Washburn(LW)渗吸模型
毛细水主要受到基质吸力Fcap、毛细管侧壁的黏性阻力Fvisco和毛细水自身重力Fgrav作用。毛细水上升过程中液体充分发展的稳态阶段在整个上升过程中占有重要地位, 此时的流体可视为层流, 尤其是通过一个等截面圆管的流体流动被认为是Hagen-Poiseuille流动[19], 其流动的控制方程可直接由纳维-斯托克斯方程(Navier-Stokes)[20]求得。根据计算有:
(1) 式中: γ——毛细水液面张力;
φ——接触角;
R——平均空隙半径;
η——流体黏度;
ρ——毛细水密度;
g——重力加速度;
t——时间;
h——毛细水上升高度。
在黏性力作用阶段, Lucas和Wash burn忽略式(1)中惯性力和重力的作用, 提出了该阶段的简化模型(LW):
(2) 对于黏性力-重力作用阶段, Washburn在考虑了毛细水重力、黏性阻力和基质吸力作用, 求解出式(1)的隐形解:
(3) 式中,
当基质吸力和毛细水重力相平衡时, 毛细水上升到最大高度, 可以求得最大高度heq为:
(4) 毛细水达到最大高度后, 其运移过程趋于平衡, 此时其表现出的特征称为毛细水赋存特征, 常用土壤水分特征曲线表征。
1.2 土壤水分特征曲线Van Genuchten模型
土壤水分特征曲线又名土壤持水曲线(soil water retention curve, SWRC), 表征土壤中含水率与势能之间的关系, 是研究非饱和土壤水分的保持能力和运移规律所用到的基本特性曲线, 本文选用Van Genuchten模型以描述土水特征曲线[21]:
(5) (6) (7) (8) 式中: θ(h)——土壤体积含水率;
θr, θs——残余含水率、饱和含水率/(cm3·cm-3);
α, m, n——土壤水分曲线参数;
h——土壤水吸力/cm;
K(h), KS——饱和渗透系数;
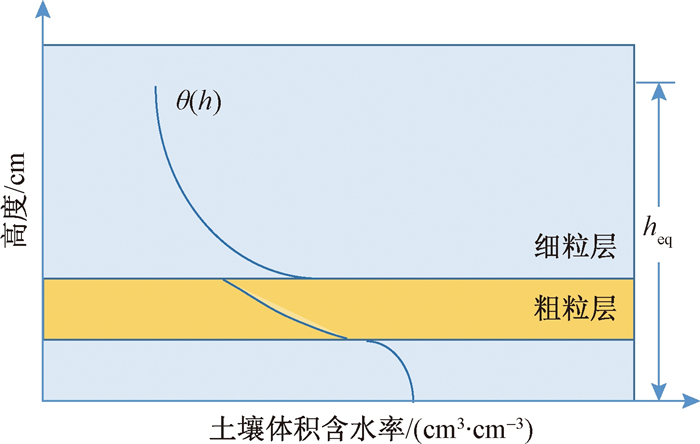
在毛细水上升过程中, 当砂土层覆盖黏土层时, 水分在界面处运移速率取决于两层土壤的土壤持水曲线(soil water retention curve, SWRC), 该曲线反映了土壤水的基质势(或土壤水吸力)与土壤含水率的变化关系, 主要受到土壤颗粒粒径、矿物成分、孔隙率、孔径大小、容重等因素影响。砂土和黏土初始含水率相近, 但下层黏土的基质吸力明显高于上层砂土的基质吸力[24]。因此, 当下部毛细水湿润锋上升到界面处时, 不能立即进入上部砂层, 水流会在界面处滞留。直至黏土基质吸力随含水率升高而降低, 并低于上层砂土的基质吸力时, 毛细水流才会越过界面继续向上运动[24~27], 该现象即为“毛细屏障作用”。
图 1显示了在毛细水湿润锋穿过砂土层达到平衡状态后层状土壤剖面中含水率的分布。当毛细水进入砂土层后, 由于砂土的基质势低于黏土, 因此, 在毛细水运移过程稳定后, 整个土壤剖面的含水率不连续, 砂土层的含水率会出现低于黏土层的突变。
1.2 土壤水分特征曲线Van Genuchten模型
土壤水分特征曲线又名土壤持水曲线(soil water retention curve, SWRC), 表征土壤中含水率与势能之间的关系, 是研究非饱和土壤水分的保持能力和运移规律所用到的基本特性曲线, 本文选用Van Genuchten模型以描述土水特征曲线[21]:
(5) (6) (7) (8) 式中: θ(h)——土壤体积含水率;
θr, θs——残余含水率、饱和含水率/(cm3·cm-3);
α, m, n——土壤水分曲线参数;
h——土壤水吸力/cm;
K(h), KS——饱和渗透系数;
在毛细水上升过程中, 当砂土层覆盖黏土层时, 水分在界面处运移速率取决于两层土壤的土壤持水曲线(soil water retention curve, SWRC), 该曲线反映了土壤水的基质势(或土壤水吸力)与土壤含水率的变化关系, 主要受到土壤颗粒粒径、矿物成分、孔隙率、孔径大小、容重等因素影响。砂土和黏土初始含水率相近, 但下层黏土的基质吸力明显高于上层砂土的基质吸力[24]。因此, 当下部毛细水湿润锋上升到界面处时, 不能立即进入上部砂层, 水流会在界面处滞留。直至黏土基质吸力随含水率升高而降低, 并低于上层砂土的基质吸力时, 毛细水流才会越过界面继续向上运动[24~27], 该现象即为“毛细屏障作用”。
图 1显示了在毛细水湿润锋穿过砂土层达到平衡状态后层状土壤剖面中含水率的分布。当毛细水进入砂土层后, 由于砂土的基质势低于黏土, 因此, 在毛细水运移过程稳定后, 整个土壤剖面的含水率不连续, 砂土层的含水率会出现低于黏土层的突变。
1.3 AHFO技术测试原理
本文采用AHFO法测量毛细水运移过程与赋存特征。主动加热光纤法(Actively heated fiber optic method, 简称AHFO), 是利用热耗散原理测量土壤中含水率[28]。通过AHFO法测得的温度值满足:
(9) 式中: T——AHFO法测得土壤温度/ ℃;
P——单位长度加热功率/(J·m-1·s1);
λ——土壤有效导热系数;
D——线性热源长度, 本文中即为测管长度/m;
rb——线性热源半径, 本文中即为测管半径/m;
Rb——土壤热阻系数/(K·m·W-1);
T0——土壤初始温度/℃;
t——加热时间/s;
α——所测土壤热扩散系数/(m2·s1)。
式(9)可以简化为[28]:
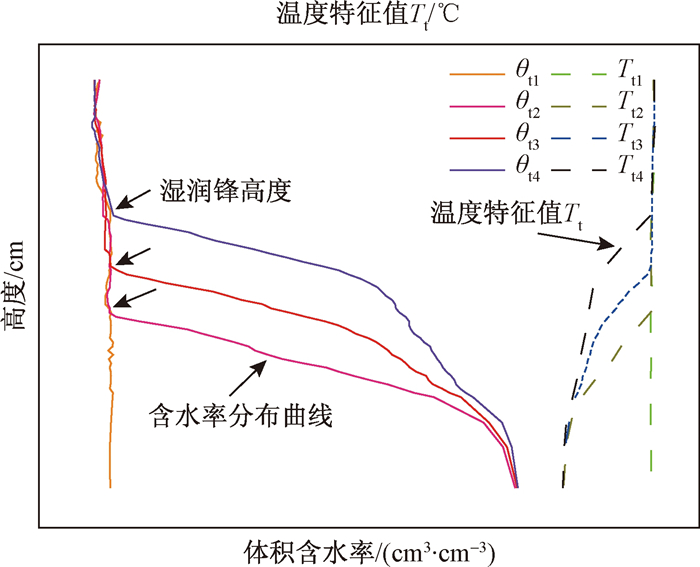
(10) 土壤的导热系数与其含水率有关, 含水率越高, 土壤的导热能力越强, 导热系数越大, 在相同功率下加热相同时间时所达到的温度越低。Sayde等[29]研究建议, 将温度特征值和土壤的含水率建立函数关系, 根据所测温度特征值直接推算土壤含水率, 可以大大降低求解误差。碳纤维加热光缆周边形成的温度场升温梯度稳定时, 选取某个时间段[t1, t2]计算单位时间平均温度升高值, 该平均温度升高值即为温度特征值Tt[30]。如图 2所示, 测量时通过碳纤维或金属材料对土体施加温度场, 利用分布式光纤监测周围土体温度特征值Tt, 根据温度特征值Tt与体积含水率θ的函数关系就可以计算出土壤的体积含水率θ。根据土壤含水率θ分布曲线, 箭头所指含水率突增点为湿润锋所达高度, 即毛细水上升高度。
曹鼎峰等[17]通过测试证明, 单用指数函数、幂函数或对数函数模型不能满足整个时刻的需求, 而分段函数模型具有测试精度高、标定简单、工程领域实用性强的优点。所以本文采用分段函数模型, 根据文献[17]研究结果, 含水率较低时采用对数函数, 含水率较高时采用线性函数, 其函数表达式为:
(11) 式中: θc——界限含水率, 即Tt-θ-h曲线上曲率半径最小点所对应的含水率;
θs——饱和含水率;
a, b, c, k, d——常参数。
试验前通过取样烘干测得的含水率与温度特征值拟合出a, b, c, k, d等5个参数。
1.3 AHFO技术测试原理
本文采用AHFO法测量毛细水运移过程与赋存特征。主动加热光纤法(Actively heated fiber optic method, 简称AHFO), 是利用热耗散原理测量土壤中含水率[28]。通过AHFO法测得的温度值满足:
(9) 式中: T——AHFO法测得土壤温度/ ℃;
P——单位长度加热功率/(J·m-1·s1);
λ——土壤有效导热系数;
D——线性热源长度, 本文中即为测管长度/m;
rb——线性热源半径, 本文中即为测管半径/m;
Rb——土壤热阻系数/(K·m·W-1);
T0——土壤初始温度/℃;
t——加热时间/s;
α——所测土壤热扩散系数/(m2·s1)。
式(9)可以简化为[28]:
(10) 土壤的导热系数与其含水率有关, 含水率越高, 土壤的导热能力越强, 导热系数越大, 在相同功率下加热相同时间时所达到的温度越低。Sayde等[29]研究建议, 将温度特征值和土壤的含水率建立函数关系, 根据所测温度特征值直接推算土壤含水率, 可以大大降低求解误差。碳纤维加热光缆周边形成的温度场升温梯度稳定时, 选取某个时间段[t1, t2]计算单位时间平均温度升高值, 该平均温度升高值即为温度特征值Tt[30]。如图 2所示, 测量时通过碳纤维或金属材料对土体施加温度场, 利用分布式光纤监测周围土体温度特征值Tt, 根据温度特征值Tt与体积含水率θ的函数关系就可以计算出土壤的体积含水率θ。根据土壤含水率θ分布曲线, 箭头所指含水率突增点为湿润锋所达高度, 即毛细水上升高度。
曹鼎峰等[17]通过测试证明, 单用指数函数、幂函数或对数函数模型不能满足整个时刻的需求, 而分段函数模型具有测试精度高、标定简单、工程领域实用性强的优点。所以本文采用分段函数模型, 根据文献[17]研究结果, 含水率较低时采用对数函数, 含水率较高时采用线性函数, 其函数表达式为:
(11) 式中: θc——界限含水率, 即Tt-θ-h曲线上曲率半径最小点所对应的含水率;
θs——饱和含水率;
a, b, c, k, d——常参数。
试验前通过取样烘干测得的含水率与温度特征值拟合出a, b, c, k, d等5个参数。
2. 室内试验
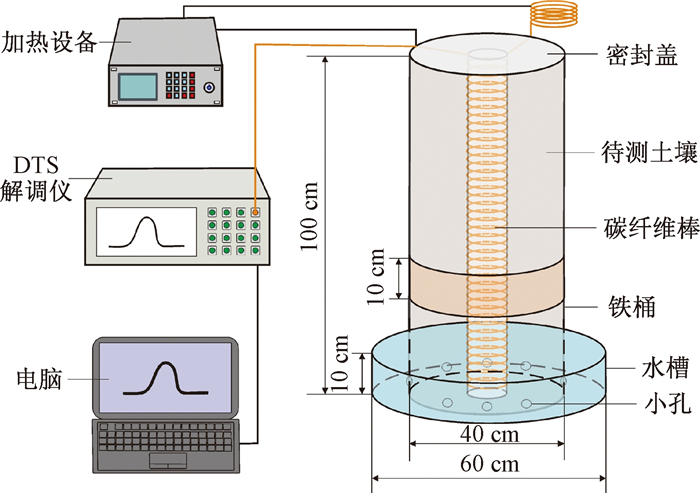
为了测量均质土和层状土中毛细水运移规律, 评价分析LW模型在毛细水运移表述中的误差, 设计了均质土和层状土的毛细水上升模型试验。试验装置如图 3所示。试验装置主要包括铁桶和水槽。铁桶高度100 cm, 直径40 cm, 上部有桶盖防止水分蒸发, 下部在距桶底3 cm处铁桶侧面均匀设置8个半径2 cm小孔, 保证铁桶内部和水槽内保持相同水位高度。铁桶放置于1个深度为10 cm、直径60 cm水槽中。为防止土壤堵塞下部小孔, 在桶底铺设厚10 cm、粒径4~8 mm砾石层作为反滤层。在砾石层上覆1层纱布防止上部黏土进入。
为了提高光纤测量的空间分辨率, 将碳纤维加热光缆紧密缠绕直径50 mm的PVC管, 制成碳纤维感测光缆测管, 简称测管, 设备与测管如图 4所示。并在测管外侧紧套热缩管防止水分沿光缆上移产生误差。光纤的空间分辨率为1 m, 因此沿测管方向空间分辨率达到20 mm, 满足室内试验要求。
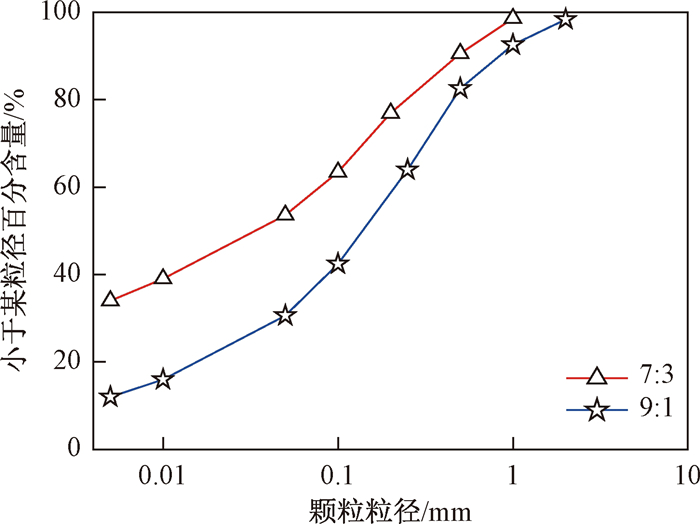
试验所采用的工业砂和高岭土初始含水率分别为7.7%、4.7%, 工业砂干密度为1.53 g/cm3, 高岭土干密度为2.53 g/cm3, 工业砂与高岭土按照9∶1、7∶3比例均匀混合后土壤颗粒级配曲线如图 5所示。本次所用DTS解调仪主要技术指标如表 1所示。
表 1 DTS解调仪主要技术指标Table 1. Main technical indexes of DTS demodulator
试验时将工业砂和高岭土分别按照比例9∶1和7∶3均匀混合, 得到砂土和黏土材料。在桶底砾石层上覆盖一层纱布, 将光纤测管埋置于铁桶正中心固定, 再将试验材料分层装满铁桶, 每次装填10 cm后击实, 并做刨毛处理, 减小分层装填对模型整体性的影响。对于均质土模型, 分别直接用按9∶1和7∶3比例均匀混合的材料分层填装满铁桶; 对于层状土模型, 先填装厚度20 cm按7∶3比例均匀混合的黏土, 再填装厚度10 cm按9∶1比例均匀混合的砂土, 再用黏土将铁桶填装满。在初始状态下测得模型中土壤的初始含水率, 然后向水槽中持续加水保持满水状态。前24 h通过AHFO法每1 h测试1次含水率, 24 h后每隔12 h左右测1次含水率并取样。
2. 室内试验
为了测量均质土和层状土中毛细水运移规律, 评价分析LW模型在毛细水运移表述中的误差, 设计了均质土和层状土的毛细水上升模型试验。试验装置如图 3所示。试验装置主要包括铁桶和水槽。铁桶高度100 cm, 直径40 cm, 上部有桶盖防止水分蒸发, 下部在距桶底3 cm处铁桶侧面均匀设置8个半径2 cm小孔, 保证铁桶内部和水槽内保持相同水位高度。铁桶放置于1个深度为10 cm、直径60 cm水槽中。为防止土壤堵塞下部小孔, 在桶底铺设厚10 cm、粒径4~8 mm砾石层作为反滤层。在砾石层上覆1层纱布防止上部黏土进入。
为了提高光纤测量的空间分辨率, 将碳纤维加热光缆紧密缠绕直径50 mm的PVC管, 制成碳纤维感测光缆测管, 简称测管, 设备与测管如图 4所示。并在测管外侧紧套热缩管防止水分沿光缆上移产生误差。光纤的空间分辨率为1 m, 因此沿测管方向空间分辨率达到20 mm, 满足室内试验要求。
试验所采用的工业砂和高岭土初始含水率分别为7.7%、4.7%, 工业砂干密度为1.53 g/cm3, 高岭土干密度为2.53 g/cm3, 工业砂与高岭土按照9∶1、7∶3比例均匀混合后土壤颗粒级配曲线如图 5所示。本次所用DTS解调仪主要技术指标如表 1所示。
表 1 DTS解调仪主要技术指标Table 1. Main technical indexes of DTS demodulator
试验时将工业砂和高岭土分别按照比例9∶1和7∶3均匀混合, 得到砂土和黏土材料。在桶底砾石层上覆盖一层纱布, 将光纤测管埋置于铁桶正中心固定, 再将试验材料分层装满铁桶, 每次装填10 cm后击实, 并做刨毛处理, 减小分层装填对模型整体性的影响。对于均质土模型, 分别直接用按9∶1和7∶3比例均匀混合的材料分层填装满铁桶; 对于层状土模型, 先填装厚度20 cm按7∶3比例均匀混合的黏土, 再填装厚度10 cm按9∶1比例均匀混合的砂土, 再用黏土将铁桶填装满。在初始状态下测得模型中土壤的初始含水率, 然后向水槽中持续加水保持满水状态。前24 h通过AHFO法每1 h测试1次含水率, 24 h后每隔12 h左右测1次含水率并取样。
3. 试验结果
3. 试验结果
3.1 含水率与温度特征值标定
已知温度特征值Tt与土壤含水率θ之间的函数表达形式, 参照文献[17]取样烘干分段拟合的标定方式, 分别拟合出工业砂与高岭土按照9∶1、7∶3均匀混合土函数表达式中的常参数a, b, c, k, d, 其表达式为:
9∶1土样
(12) 7∶3土样
(13) 3.1 含水率与温度特征值标定
已知温度特征值Tt与土壤含水率θ之间的函数表达形式, 参照文献[17]取样烘干分段拟合的标定方式, 分别拟合出工业砂与高岭土按照9∶1、7∶3均匀混合土函数表达式中的常参数a, b, c, k, d, 其表达式为:
9∶1土样
(12) 7∶3土样
(13) 3.2 土壤含水率运移与分布
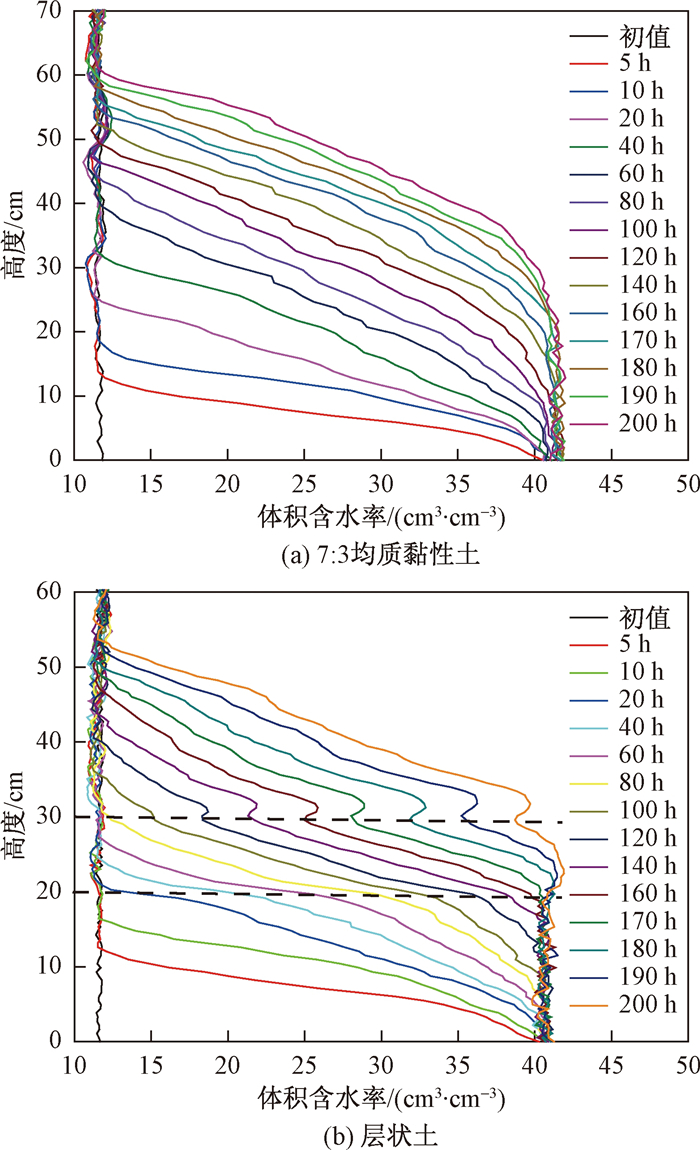
基于AHFO技术测得不同时刻均质土与层状土剖面中土壤含水率分布如图 6所示, 图 6(a)为工业砂和高岭土按照比例7∶3均匀混合所得均质黏性土中不同时刻体积含水率分布曲线, 图 6(b)为层状土中不同时刻体积含水率分布曲线, 图中水平虚线为分层界面, 0~20 cm为7∶3均质黏土, 20~30 cm为9∶1均质砂土, 30~100 cm为7∶3均质黏土。图中含水率突增点所对应高度即为毛细水湿润锋所达到高度。可以看出, 随着时间延长, 两种土毛细水上升高度逐渐增高, 湿润锋以下土壤含水率也逐渐增大。而湿润锋上升速率和含水率增长速率逐渐降低。主要是因为随着毛细水量的增加, 重力势增大, 基质势不变, 毛细水所受向上驱动力减小。当含水率增加到重力势与基质势相同时, 向上驱动力为零, 毛细水达到最大上升高度。在毛细水湿润锋达到20 cm前, 两者运移规律相同, 但达到20 cm后, 层状土砂土层中含水率急剧下降, 远低于均质土中同层位土壤含水率。这是因为砂土基质吸力突然变小, 其持水能力降低。而且湿润锋超过30 cm后, 从下到上均质土中含水率缓慢下降, 但层状土中含水率却先升高后降低。这是因为上层黏土层基质吸力变大, 持水能力增强。
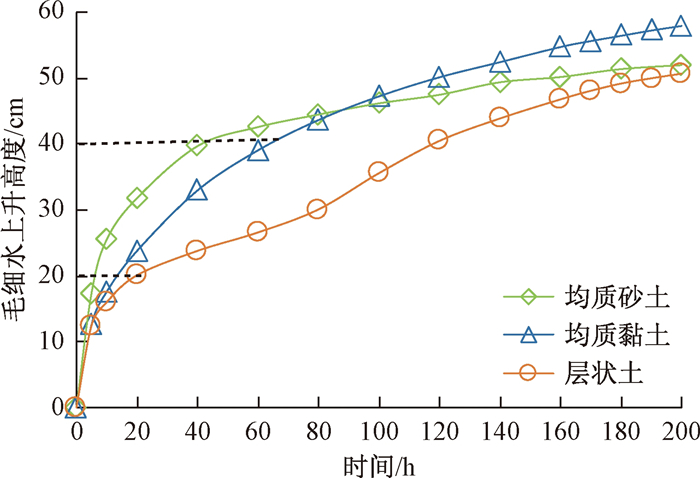
为了便于观察分析毛细水湿润锋随时间升高规律, 由图 6中含水率分布曲线绘制出均质砂土、均质黏土和层状土湿润锋高度随时间变化曲线, 即毛细水上升高度随时间变化关系曲线(图 7)。
由图 7可以发现, 当毛细水上升到20 cm时, 毛细水湿润锋到达黏土层(下部)与砂土层(上部)界面高度, 均质黏土和均质砂土中毛细水持续稳定上升, 20 h时毛细水分别上升到25 cm和30 cm, 但层状土中毛细水发生滞留与减缓, 20 h时毛细水仍滞留在20 cm高度。原因是下层黏土的基质吸力大于上层砂土, 毛细水不能立即进入砂土层。但是界面以下黏土中水分持续增加, 基质吸力不断减小, 直至下层黏土中基质吸力随着含水率的升高而下降到与上层砂土的基质吸力相同时, 毛细水才能越过界面继续向上运移进入砂土层, 40 h时毛细水达到25 cm。该现象即“毛细屏障作用”。
80 h后, 均质黏土和均质砂土中毛细水高度均已超过40 cm, 上升速率缓慢, 而层状土中毛细水达到30 cm进入黏土层, 其上升速率加快, 与均值土毛细水高度差距逐渐减小。根据田町正誉[31]的解释, 当小孔径毛细管连通在大孔径毛细管之上时, 毛细水的上升速率明显加快, 是因为砂土层中大孔径毛细管促进了水分在黏土小孔径毛细管中的运动。究其本质, 是由于在接近地下水位处, 土壤剖面的含水量较大, 砂土的导水率明显大于黏土所致[32]。
对比均质砂土与均质黏土上升曲线, 85 h前黏土中毛细水上升速率低于砂土, 根据张志权[33]的研究, 毛细水前期的上升速度与土壤毛细管通畅性相关, 黏粒含量越高, 毛细管截面内被黏粒强烈吸附的结合水越多, 阻碍了自由水向上运动, 所以毛细水上升速度越慢, 与本试验实际测得的结果相同。
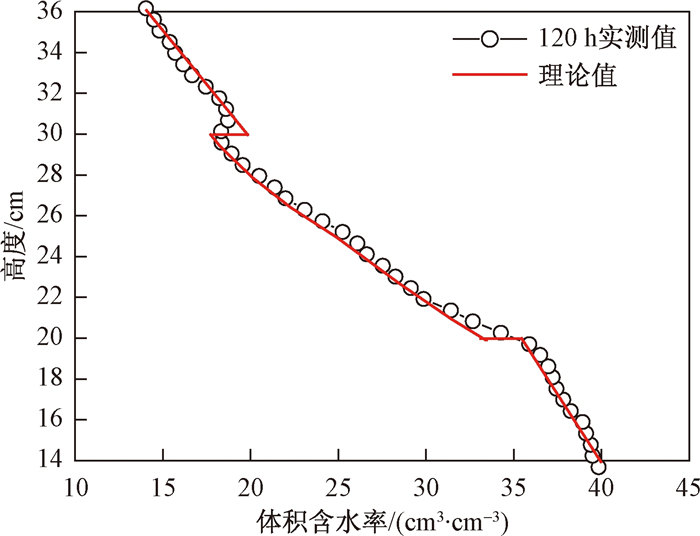
根据Van Genuchten模型理论, 在黏土层与砂土层界面处含水率会发生突变。而图 6(b)中实际测得的结果却是连续缓变的。选取120 h实测界面处含水率与理论值绘制在图 8中, 可以看出在层内含水率实测值与理论值很吻合, 但是在界面处吻合度较低。这是由AHFO技术测量原理导致的。已知测管空间分辨率为2 cm, 即测管每一点监测值为上下各1 cm内监测值的平均值, 因此在含水率的突变处由光纤测管测得的突变程度是低于实际突变程度的。
3.2 土壤含水率运移与分布
基于AHFO技术测得不同时刻均质土与层状土剖面中土壤含水率分布如图 6所示, 图 6(a)为工业砂和高岭土按照比例7∶3均匀混合所得均质黏性土中不同时刻体积含水率分布曲线, 图 6(b)为层状土中不同时刻体积含水率分布曲线, 图中水平虚线为分层界面, 0~20 cm为7∶3均质黏土, 20~30 cm为9∶1均质砂土, 30~100 cm为7∶3均质黏土。图中含水率突增点所对应高度即为毛细水湿润锋所达到高度。可以看出, 随着时间延长, 两种土毛细水上升高度逐渐增高, 湿润锋以下土壤含水率也逐渐增大。而湿润锋上升速率和含水率增长速率逐渐降低。主要是因为随着毛细水量的增加, 重力势增大, 基质势不变, 毛细水所受向上驱动力减小。当含水率增加到重力势与基质势相同时, 向上驱动力为零, 毛细水达到最大上升高度。在毛细水湿润锋达到20 cm前, 两者运移规律相同, 但达到20 cm后, 层状土砂土层中含水率急剧下降, 远低于均质土中同层位土壤含水率。这是因为砂土基质吸力突然变小, 其持水能力降低。而且湿润锋超过30 cm后, 从下到上均质土中含水率缓慢下降, 但层状土中含水率却先升高后降低。这是因为上层黏土层基质吸力变大, 持水能力增强。
为了便于观察分析毛细水湿润锋随时间升高规律, 由图 6中含水率分布曲线绘制出均质砂土、均质黏土和层状土湿润锋高度随时间变化曲线, 即毛细水上升高度随时间变化关系曲线(图 7)。
由图 7可以发现, 当毛细水上升到20 cm时, 毛细水湿润锋到达黏土层(下部)与砂土层(上部)界面高度, 均质黏土和均质砂土中毛细水持续稳定上升, 20 h时毛细水分别上升到25 cm和30 cm, 但层状土中毛细水发生滞留与减缓, 20 h时毛细水仍滞留在20 cm高度。原因是下层黏土的基质吸力大于上层砂土, 毛细水不能立即进入砂土层。但是界面以下黏土中水分持续增加, 基质吸力不断减小, 直至下层黏土中基质吸力随着含水率的升高而下降到与上层砂土的基质吸力相同时, 毛细水才能越过界面继续向上运移进入砂土层, 40 h时毛细水达到25 cm。该现象即“毛细屏障作用”。
80 h后, 均质黏土和均质砂土中毛细水高度均已超过40 cm, 上升速率缓慢, 而层状土中毛细水达到30 cm进入黏土层, 其上升速率加快, 与均值土毛细水高度差距逐渐减小。根据田町正誉[31]的解释, 当小孔径毛细管连通在大孔径毛细管之上时, 毛细水的上升速率明显加快, 是因为砂土层中大孔径毛细管促进了水分在黏土小孔径毛细管中的运动。究其本质, 是由于在接近地下水位处, 土壤剖面的含水量较大, 砂土的导水率明显大于黏土所致[32]。
对比均质砂土与均质黏土上升曲线, 85 h前黏土中毛细水上升速率低于砂土, 根据张志权[33]的研究, 毛细水前期的上升速度与土壤毛细管通畅性相关, 黏粒含量越高, 毛细管截面内被黏粒强烈吸附的结合水越多, 阻碍了自由水向上运动, 所以毛细水上升速度越慢, 与本试验实际测得的结果相同。
根据Van Genuchten模型理论, 在黏土层与砂土层界面处含水率会发生突变。而图 6(b)中实际测得的结果却是连续缓变的。选取120 h实测界面处含水率与理论值绘制在图 8中, 可以看出在层内含水率实测值与理论值很吻合, 但是在界面处吻合度较低。这是由AHFO技术测量原理导致的。已知测管空间分辨率为2 cm, 即测管每一点监测值为上下各1 cm内监测值的平均值, 因此在含水率的突变处由光纤测管测得的突变程度是低于实际突变程度的。
3.3 Lucas-Washburn渗吸模型预测与修正
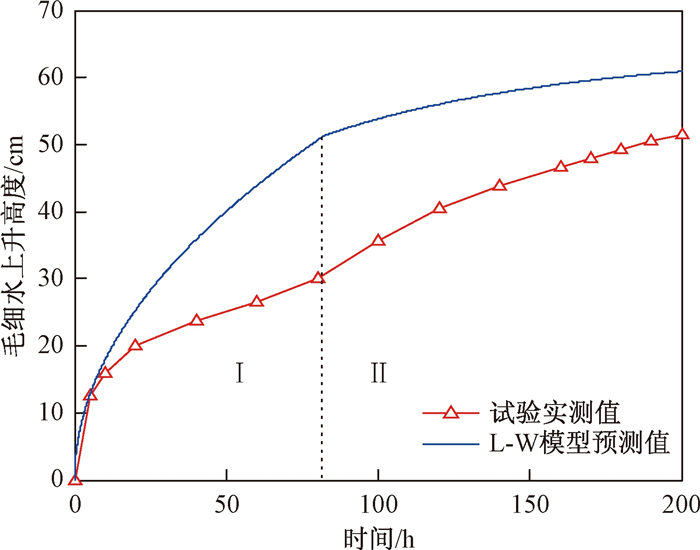
通过Lucas-Washburn模型可以计算预测毛细水湿润锋上升高度, 根据文献[7]中所给出ρ, γ, φ, η的经验值, 并通过文献[34]中给出的平均空隙直径D0与d20和孔隙率之间的关系D0=0.63nd20, 代入毛细水在黏性力作用阶段和黏性力-重力作用阶段的表达式(2)和式(3), 绘制出Lucas-Washburn渗吸模型预测曲线和层状土湿润锋高度实测值曲线如图 9所示。
根据图 9层状土中毛细水湿润锋实测高度和Lucas-Washburn模型预测值, 在高度达到20 cm前模型预测值较准确, 但毛细水进入砂土层后该模型无法预测湿润锋高度。一是因为砂土层减缓了毛细水上升速度, 二是因为毛细水穿过砂土层重新进入上层黏土层后, 下部砂土层导水率加大, 有利于毛细水运移。据此, 为了描述毛细水在上层黏土中运移规律, 本文对Lucas-Washburn模型进行修正。由于上述两点原因的主要影响因素是毛细管径, 因此, 定义穿过砂土层后上层黏土的等效毛细管半径R为:
(14) 式中: R1, R2——砂土和黏土的平均空隙半径/m;
D1, D2——砂土层厚度和毛细水进入上部黏土层高度/cm。
则Lucas-Washburn模型黏性力-重力作用阶段修正后Improved Lucas-Washburn模型(ILW模型)表达式为:
(15) (16) 将已知黏土和砂土的水土特征参数代入, 可以得到毛细水在层状土中的运移方程为:
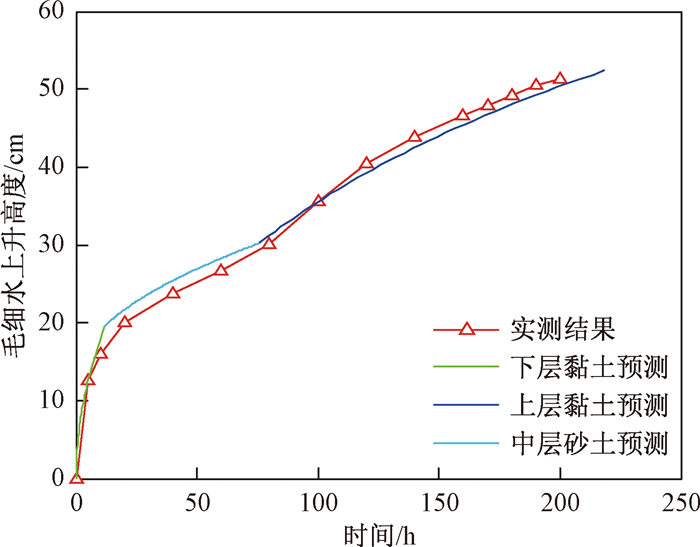
(17) 通过MATLAB绘制出实测结果与修正拟合结果曲线如图 10所示。修正后的结果精度大大提高, 与实测值也很接近。可以精确描述层状土中毛细水的上升过程。
对比图 9中修正前Lucas-Washburn模型(LW模型)预测曲线和图 10中修正后Improved Lucas-Washburn模型(ILW模型)预测曲线, 修正等效平均空隙半径R后的曲线精度较高, 能够有效预测层状土中毛细水上升规律, 对层状土中毛细水运移规律的预测具有较高参考价值。
3.3 Lucas-Washburn渗吸模型预测与修正
通过Lucas-Washburn模型可以计算预测毛细水湿润锋上升高度, 根据文献[7]中所给出ρ, γ, φ, η的经验值, 并通过文献[34]中给出的平均空隙直径D0与d20和孔隙率之间的关系D0=0.63nd20, 代入毛细水在黏性力作用阶段和黏性力-重力作用阶段的表达式(2)和式(3), 绘制出Lucas-Washburn渗吸模型预测曲线和层状土湿润锋高度实测值曲线如图 9所示。
根据图 9层状土中毛细水湿润锋实测高度和Lucas-Washburn模型预测值, 在高度达到20 cm前模型预测值较准确, 但毛细水进入砂土层后该模型无法预测湿润锋高度。一是因为砂土层减缓了毛细水上升速度, 二是因为毛细水穿过砂土层重新进入上层黏土层后, 下部砂土层导水率加大, 有利于毛细水运移。据此, 为了描述毛细水在上层黏土中运移规律, 本文对Lucas-Washburn模型进行修正。由于上述两点原因的主要影响因素是毛细管径, 因此, 定义穿过砂土层后上层黏土的等效毛细管半径R为:
(14) 式中: R1, R2——砂土和黏土的平均空隙半径/m;
D1, D2——砂土层厚度和毛细水进入上部黏土层高度/cm。
则Lucas-Washburn模型黏性力-重力作用阶段修正后Improved Lucas-Washburn模型(ILW模型)表达式为:
(15) (16) 将已知黏土和砂土的水土特征参数代入, 可以得到毛细水在层状土中的运移方程为:
(17) 通过MATLAB绘制出实测结果与修正拟合结果曲线如图 10所示。修正后的结果精度大大提高, 与实测值也很接近。可以精确描述层状土中毛细水的上升过程。
对比图 9中修正前Lucas-Washburn模型(LW模型)预测曲线和图 10中修正后Improved Lucas-Washburn模型(ILW模型)预测曲线, 修正等效平均空隙半径R后的曲线精度较高, 能够有效预测层状土中毛细水上升规律, 对层状土中毛细水运移规律的预测具有较高参考价值。
4. 结论
(1) 通过主动加热光纤法(AHFO)分布式测得均质土和层状土整个剖面含水率, 分析发现毛细水在达到下部黏土层与砂土层界面时产生“毛细屏障作用”, 砂土层中毛细水含水率急剧下降。而砂土层与上部黏土层界面处含水率突增, 平稳后砂土层含水率低于同层位均质土含水率。这主要是由于层状土中基质吸力变化造成的。
(2) 当毛细水越过砂土层后, 黏土层中毛细水上升速率大于同时刻均质土中毛细水上升速率, 是因为砂土层的导水率明显大于黏土层, 砂土黏性阻力小于黏土, 毛细水的驱动力大于均质土。
(3) Lucas-Washburn渗吸模型可以有效准确预测均质土中毛细水湿润锋上升高度。层状土由于“毛细屏障作用”和下部土层导水率的增大, Lucas-Washburn渗吸模型预测值远远高于实测值, 无法有效预测层状土中毛细水上升规律。
(4) 根据层状土中毛细水运移特征对Lucas-Washburn渗吸模型中平均空隙半径R进行了修正, 提出等效毛细管半径
4. 结论
(1) 通过主动加热光纤法(AHFO)分布式测得均质土和层状土整个剖面含水率, 分析发现毛细水在达到下部黏土层与砂土层界面时产生“毛细屏障作用”, 砂土层中毛细水含水率急剧下降。而砂土层与上部黏土层界面处含水率突增, 平稳后砂土层含水率低于同层位均质土含水率。这主要是由于层状土中基质吸力变化造成的。
(2) 当毛细水越过砂土层后, 黏土层中毛细水上升速率大于同时刻均质土中毛细水上升速率, 是因为砂土层的导水率明显大于黏土层, 砂土黏性阻力小于黏土, 毛细水的驱动力大于均质土。
(3) Lucas-Washburn渗吸模型可以有效准确预测均质土中毛细水湿润锋上升高度。层状土由于“毛细屏障作用”和下部土层导水率的增大, Lucas-Washburn渗吸模型预测值远远高于实测值, 无法有效预测层状土中毛细水上升规律。
(4) 根据层状土中毛细水运移特征对Lucas-Washburn渗吸模型中平均空隙半径R进行了修正, 提出等效毛细管半径
-
表 1 DTS解调仪主要技术指标
Table 1 Main technical indexes of DTS demodulator

表 1 DTS解调仪主要技术指标
Table 1 Main technical indexes of DTS demodulator

-
[1] 蔡建超, 郁伯铭. 多孔介质自发渗吸研究进展[J]. 力学进展, 2012, 42(6): 735-754. CAI J C, YU B M. Advances in studies of spontaneous imbibition in porous media[J]. Advances in Mechanics, 2012, 42(6): 735-754. (in Chinese)
[2] Mingbin Huang, S Lee Barbour, Amin Elshorbagy, et al. Infiltration and drainage processes in multi-layered coarse soils[J]. Revue Canadienne De La Science Du Sol, 2011, 91(2): 185-197.
[3] Zornberg J G, Bouazza A, Mccartney J S. Geosynthetic capillary barriers: current state of knowledge[J]. Geosynthetics International, 2015, 17(5): 273-300.
[4] Bruch P G. Laboratory study of evaporative fluxes in homogeneous and layered soils[D]. Saskatoon: University of Saakatoon, 1993.
[5] Hill D E. Wetting front instability in layered soils[J]. Soil Science Society of America Journal, 1972, 36(5): 697-702. DOI: 10.2136/sssaj1972.03615995003600050010x
[6] Baker R S, Hillel D. Laboratory tests of a theory of fingering during infiltration into layered soils[J]. Soil Science Society of America Journal, 1990, 54(1): 20-30. DOI: 10.2136/sssaj1990.03615995005400010004x
[7] 付志文, 武海英. 土中毛细水运移阶段理论研究[J]. 工程与建设, 2013(6): 749-751. DOI: 10.3969/j.issn.1673-5781.2013.06.009 FU Z W, WU H Y. Theoretical study on the phase of capillary water migration in soil[J]. Engineering and Construction, 2013(6): 749-751. (in Chinese) DOI: 10.3969/j.issn.1673-5781.2013.06.009
[8] Julie D Zettl, S Lee Barbour, Mingbin Huang, et al. Influence of textural layering on field capacity of coarse soils[J]. Canadian Journal of Soil Science, 2011, 91(2): 133. DOI: 10.4141/cjss09117
[9] Washburn E W. Dynamics of capillary flow[J]. Phys. Rev., 1921, 17(3): 273-283. DOI: 10.1103/PhysRev.17.273
[10] Bosanquet C H. On the flow of liquids into capillary tubes[J]. Philos. Mag, 1923, 45(267): 525-531. DOI: 10.1080/14786442308634144
[11] Szekely J, Neumann A W, Chuang Y K. The rate of capillary penetration and the applicability of the Washburn equation[J]. Colloid Interface Sci., 1971, 35(2): 273-278. DOI: 10.1016/0021-9797(71)90120-2
[12] Quere D. Inertial capillarity[J]. Europhys Lett., 1997, 39(5): 533-538. DOI: 10.1209/epl/i1997-00389-2
[13] Lucas R. Rate of capillary ascension of liquids[J]. Kolloid-Zeitschrift, 1918, 23: 15-22. DOI: 10.1007/BF01461107
[14] Cai J C, Yu B M, Mei M F, et al. Capillary Rise in a Single Tortuous Capillary[J]. Chinese Physics Letters, 2010, 27(5): 148-151.
[15] 邓英春, 许永辉. 土壤水分测量方法研究综述[J]. 水文, 2007, 27(4): 20-24. DENG Y C, XU Y H. A Survey of soil moisture measurement methods[J]. Journal of China Hydrology, 2007, 27(4): 20-24. (in Chinese)
[16] 王贵彦, 史秀捧, 张建恒, 等. TDR法、中子法、重量法测定土壤含水量的比较研究[J]. 河北农业大学学报, 2000, 23(3): 23-26. DOI: 10.3969/j.issn.1000-1573.2000.03.007 WANG G Y, SHI X P, ZHANG J H, et al. Comparative study on measuring soil moisture by TDR, Neutron and Gravimetric methods[J]. Journal of Agricultural University of Hebei, 2000, 23(3): 23-26. (in Chinese) DOI: 10.3969/j.issn.1000-1573.2000.03.007
[17] 曹鼎峰, 施斌, 顾凯, 等. 土的含水率AHFO法测量中分段函数模型建立[J]. 水文地质工程地质, 2016, 43(6): 41-47. https://www.swdzgcdz.com/article/id/20160607 CAO D F, SHI B, GU K, et al. Establishment of the piecewise function model in the process of soil moisture monitoring with the AHFO method[J]. Hydrogeology & Engineering Geology, 2016, 43(6): 41-47. (in Chinese) https://www.swdzgcdz.com/article/id/20160607
[18] 严珺凡, 施斌, 曹鼎峰, 等. 基于碳纤维加热光缆的砂性土渗流场C-DTS分布式监测试验研究[J]. 岩土力学, 2015, 36(2): 430-436. YAN J F, SHI B, CAO D F, et al. Experiment study of seepage field monitoring in sandy soil using carbon coated heating optical fiber-based C-DTS[J]. Rock and Soil Mechanics, 2015, 36(2): 430-436. (in Chinese)
[19] 高士桥. 毛细力学[M]. 北京: 科学出版社, 2010. GAO S Q. Capillary Mechanics[M]. Beijing: Science Press, 2010. (in Chinese)
[20] 德鲁·迈尔斯. 表面、界面和胶体: 原理及应用[M]. 北京: 化学工业出版社, 2005. Drew Myers. Surface, Interface and Colloid: Principles and Applications[M]. Beijing: Chemical Industry Press, 2005. (in Chinese)
[21] 肖建英, 李永涛, 王丽. 利用Van Genuchten模型拟合土壤水分特征曲线[J]. 地下水, 2007, 29(5): 46-47. DOI: 10.3969/j.issn.1004-1184.2007.05.015 XIAO J Y, LI Y T, WANG L. Fitting soil water characteristic curve based on the Van Genuchten model[J]. Ground Water, 2007, 29(5): 46-47. (in Chinese) DOI: 10.3969/j.issn.1004-1184.2007.05.015
[22] 陈卫金, 程东会, 陶伟. Van Genuchten模型参数的物理意义[J]. 水文地质工程地质, 2017, 44(6): 147-153. https://www.swdzgcdz.com/article/id/201706022 CHEN W J, CHENG D H, TAO W. Physical significance of the parameters in the Van Genuchten model[J]. Hydrogeology & Engineering Geology, 2017, 44(6): 147-153. (in Chinese) https://www.swdzgcdz.com/article/id/201706022
[23] 王小华, 贾克力, 刘景辉, 等. Van Genuchten模型在土壤水分特征曲线拟合分析中的应用[J]. 干旱地区农业研究, 2009, 27(2): 179-183. WANG X H, JIA K L, LIU J H, et al. Application of Van Genuchten model to analysis of soil moisture characteristic curve[J]. Agricultural research in Arid Areas, 2009, 27(2): 179-183. (in Chinese)
[24] Li X, Chang S X, Salifu K F. Soil texture and layering effects on water and salt dynamics in the presence of a water table: a review[J]. Environmental Reviews, 2014, 22(1): 1-10. DOI: 10.1139/er-2013-0013
[25] 史文娟, 汪志荣, 沈冰, 等. 夹砂层土体构型毛管水上升的实验研究[J]. 水土保持学报, 2004, 18(6): 167-170. DOI: 10.3321/j.issn:1009-2242.2004.06.041 SHI W J, WANG Z R, SHEN B, et al. Soil capillary water upward movement from sand layered soil column[J]. Journal of Soil And Water Conservation, 2004, 18(6): 167-170. (in Chinese) DOI: 10.3321/j.issn:1009-2242.2004.06.041
[26] 史文娟, 沈冰, 汪志荣, 等. 层状土壤毛管水最大上升高度分析[J]. 干旱地区农业研究, 2007, 25(1): 94-97. DOI: 10.3321/j.issn:1000-7601.2007.01.019 SHI W J, SHEN B, WANG Z R, et al. Analysis of maximum rising height of capillary water in layered soil[J]. Agricultural research in Arid Areas, 2007, 25(1): 94-97. (in Chinese) DOI: 10.3321/j.issn:1000-7601.2007.01.019
[27] 常琛朝, 程东会, 钱康. 渭河咸阳段非饱和层状沉积物中水分分布特征[J]. 中国水土保持科学, 2017, 15(4): 104-110. CHANG S C, CHENG D H, QIAN K. Water content distribution of unsaturated layered sediments of Weihe River in Xianyang section[J]. Science of Soil and Water Conservation, 2017, 15(4): 104-110. (in Chinese)
[28] Florides G, Kalogirou S. First in situ determination of the thermal performance of a U-pipe borehole heat exchanger, in Cyprus[J]. Applied Thermal Engineering, 2008, 28(2-3): 157-163. DOI: 10.1016/j.applthermaleng.2007.03.026
[29] Sayde C, Gregory C, Gil-Rodriguez M, et al. Feasibility of soil moisture monitoring with heated fiber optics[J]. Water Resources Research, 2010, 46(6): 2840-2849.
[30] 曹鼎峰, 施斌, 严珺凡, 等. 基于C-DTS的土壤含水率分布式测定方法研究[J]. 岩土工程学报, 2014, 36(5): 910-915. CAO D F, SHI B, YAN J F, et al. Distributed method for measuring moisture content of soils based on C-DTS[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(5): 910-915. (in Chinese)
[31] 田町正誉. 土壤と水との関系特に毛管现象及び渗透に就いて[J]. 农业土木研究, 1931, 3(1): 1-29. Tamachi Tadashi. Relationship between soil and water especially on capillary phenomena and penetration [J] Agricultural Civil Engineering Research, 1931, 3(1): 1-29.
[32] 李韵珠, 胡克林. 蒸发条件下黏土层对土壤水和溶质运移影响的模拟[J]. 土壤学报, 2004, 41(4): 493-502. DOI: 10.3321/j.issn:0564-3929.2004.04.001 LI Y Z, HU K L. Simulation of effects of clay layer on soil water and solute transport under evaporation conditions[J], Acta Pedologica Sinica, 2004, 41(4): 493-502. (in Chinese) DOI: 10.3321/j.issn:0564-3929.2004.04.001
[33] 张志权. 不同粉黏粒含量盐渍土的工程性质研究[D]. 西安: 长安大学, 2004. ZHANG Z Q. Study on engineering properties of saline soils with different clay concentrations[D]. Xi'an: Chang'an University, 2004. (in Chinese)
[34] 崔荣方, 陈建生, 许霆. 无黏性土粒径特征对其渗透性的影响[J]. 山西建筑, 2006, 32(6): 97-98. CUI R F, CHEN J S. XU T. Influence of particle size characteristics of non-cohesive soil on its permeability[J]. Shanxi Architecture, 2006, 32(6): 97-98. (in Chinese)
-
期刊类型引用(5)
1. 刘泳佚,史婷婷,王清,刘添文,刘亚磊,李梦茹. 江汉平原过渡带黏性层状土弥散试验与模拟研究. 水文地质工程地质. 2023(01): 41-50 .  本站查看
本站查看
2. 赵金召,李予红,孙闪闪,刘玉,康小迪. 毛细水在矿山高陡岩质边坡生态修复绿化养护中的应用研究. 节水灌溉. 2022(01): 80-84 .  百度学术
百度学术
3. 王中翰,柴金义,张宏. 层状构造土体中毛细水上升的试验研究. 内蒙古大学学报(自然科学版). 2021(02): 192-197 .  百度学术
百度学术
4. 贾俊超,张兴昌. 层状土持水性室内模拟初步研究. 水土保持研究. 2020(06): 90-93+99 .  百度学术
百度学术
5. 林雪松,王永吉,王东,王来贵,王汉勍,宋泽友,王中东,李俊岑,冯欢. 细尾矿砂非饱和渗流稳态含水率二维解析解. 中国安全生产科学技术. 2019(05): 111-116 .  百度学术
百度学术
其他类型引用(12)




 下载:
下载:

 邮件订阅
邮件订阅 RSS
RSS