Quantification and reduction of groundwater model structural uncertainty based on Gaussian process regression
-
摘要:
目前针对模型结构不确定性的研究方法主要为贝叶斯模型平均方法,而该方法受到模型权重计算困难等影响,应用受限。基于数据驱动的模型结构误差统计学习方法最近得到关注。研究采用高斯过程回归方法对地下水模型结构误差进行统计模拟,并将DREAMzs算法与高斯过程回归相结合,对地下水模型和统计模型的参数同时进行识别。基于此方法,分别以理想岩溶裂隙海水入侵过程和溶质运移柱体实验为例,进行地下水数值模拟及预测结果的不确定性分析。相对于不考虑模型结构误差条件的不确定性分析,结果表明,考虑结构误差之后,能够明显减少参数识别过程中的参数补偿影响,且能显著提高模型的预测性能。因此,基于高斯过程回归的模型结构不确定性分析可以一定程度控制地下水数值模拟的不确定性,提高模型预测可靠性。
Abstract:Nowadays, the main analysis method for groundwater model structural uncertainty is the Bayesian model averaging (BMA) method. But BMA suffers from the difficulty of model weight estimation, which makes its application infeasible. More attention is recently paid to the data-driven based model structural error analysis method. In this paper, the groundwater model structural error is statistically learnt based on Gaussian process regression, and then the parameters of the groundwater model and statistical model are identified simultaneously by combining the DREAMzs and Gaussian process regression algorithms. With this method, the uncertainty of groundwater model parameters and prediction results are analyzed. In addition, a synthetic numerical simulation of seawater intrusion in a karst fissure area and a solute transport column experiment are taken as case studies. In contrast with the uncertainty analysis without considering the model structural error, the impact of parameter compensation is significantly reduced by considering the model structural error. Moreover, the model prediction performance is also improved. Therefore, based on the model structural uncertainty analysis method proposed in this paper, the uncertainty of groundwater modeling can be reduced to some extent, as well the reliability of groundwater model prediction can be improved.
-
近年来地下水数值模拟已在科学研究与生产实践中得到广泛应用, 如地下水资源评价、海水入侵治理、地下水污染修复等方面[1]。实际地下水系统十分复杂, 限于认知程度一般对其进行简化[2-3], 由此导致了模拟及预测结果的不确定性。根据地下水数值模拟过程, 其不确定性的来源可以分为模型参数, 模型结构及观测数据的不确定性[4-5]。由于模拟结果的不确定性直接影响了相关决策的科学性, 因此有必要对地下水模型进行不确定性的定量分析与控制, 从而提高模拟结果的可靠性。
模型参数不确定性已经得到水文及地下水研究者的广泛认同, 如束龙仓等[6]考虑了水文地质参数不确定性对地下水补给量计算的影响。目前模型参数不确定性研究方法主要包括矩方法和蒙特卡洛(MC)方法[7-9]; 矩方法通过求解地下水随机偏微分方程获得变量(如水头)的均值、方差等统计量, 该方法计算量小, 但一般难以处理复杂条件的地下水模型(如不规则的边界条件、非高斯分布的模型参数), 且不能获得变量(如渗透系数、水头)的完整概率分布信息。MC方法通过在模型参数的概率分布空间内随机抽样控制模拟不确定性, 主要研究方法包括通用似然不确定性分析(GLUE)[10]和马尔科夫链蒙特卡洛模拟(MCMC)[11]。Hassan等[12]利用GLUE方法对地下水流模型参数及模型预测不确定性进行分析。陆乐等[13]利用单分量自适应Metropolis(SCAM)采样算法, 在贝叶斯框架下进行地下水流模型的参数不确定分析。Vrugt等[14-16]在原有MCMC算法的基础上提出DREAM、DREAMzs、DREAM(ABC)、MT-DREAM等算法, 提高了参数不确定性分析的效率, 并在水环境模拟不确定性分析中得到广泛应用。
模型结构不确定性表示概念模型对真实对象的刻画误差, 模型校准过程中若忽略模型结构不确定性, 将导致参数补偿(参数不确定性来补偿结构误差), 从而出现参数过矫正问题, 使得模型预测能力较差[17-18]。当前的处理方法主要有贝叶斯模型平均(BMA)[19]和基于数据驱动的结构误差统计学习方法。BMA通过建立多个地下水模型来描述地下水系统, 对这些模型的模拟结果进行加权平均处理模型结构的不确定性。目前基于BMA的模型结构不确定性研究较多, Rojas等[20]利用BMA定量分析了地下水数值模拟不确定性的组成, Parrish等[21]提出了将粒子滤波算法(PF)与BMA结合来减小模型结构误差。然而, BMA在实际应用过程中存在一些问题, 如所建立的模型具有主观性、难以考虑模型间的相关性、模型先验权重的赋值具有主观性等, 从而影响了BMA进行不确定性分析的效果。
数据驱动法(DDM)主要利用机器学习方法(如神经网络, 支持向量基回归, 随机森林, 高斯过程回归), 对模型结构误差进行统计模拟, 即使用某种统计模型来拟合模型结构误差。Demissie[22]等通过一个地下水流数值模拟案例, 分别将人工神经网络、支持向量机、决策树和基于实例权重法用于模型结构误差统计学习, 并对比了这四种方法进行模型结构不确定性分析的表现, 结果表明通过数据驱动方法进行结构误差统计学习能够提高模型预测能力, 且人工神经网络具有较优的模型结构误差统计学习表现。然而, Demissie[22]等将参数识别与结构误差统计学习分开独立进行, 参数识别阶段未考虑结构误差会导致参数识别误差(过矫正), 同时影响结构误差的统计学习。因此, 需要将模型结构与模型参数不确定性分析联合进行。Xu等[23-24]将高斯过程回归(GPR)分别用于理想与实际的地下水流模型的结构误差统计学习, 通过DREAM算法同时识别地下水流模型和统计模型参数。结果表明, GPR能够考虑结构误差时空相关性, 避免参数补偿, 提高模型预测能力。
本次研究拟使用高斯过程回归方法识别模型结构误差, 基于DREAMzs算法的MCMC模拟同时识别地下水模型和统计模型参数, 实现地下水数值模拟不确定性的控制及其定量分析。此外, 分别通过理想条件下基岩裂隙区海水入侵过程与室内柱体实验溶质运移过程的数值模拟模型, 验证不确定性分析方法的效率与可靠性。
1. 研究方法
1.1 贝叶斯参数不确定性分析
对于未考虑结构误差的模型, 通常将结构误差与测量误差作为一个整体:
(1) 式中: y(y1, …, yn)—状态向量(如水头、温度、浓度等);
M(M1, …, Mn)—模型函数;
x(x1, …, xm)—模型输入向量(m为输入向量维数);
θ(θ1, …, θd)—参数向量;
d—参数维数;
δ—误差向量包括观测误差、结构误差及参数误差。
根据贝叶斯原理, 通过观测数据y, 推导参数θ的后验分布:
(2) 式中: p(θ|y)—参数θ后验分布;
p(θ)—参数θ先验分布。
p(y|θ)为参数θ的似然函数[25]:
(3) 式中: ∑—误差向量δ的协方差矩阵。
由于p(θ|y)很难直接求得, 一般采用MCMC模拟, 抽样得到模型参数θ和模型输出的后验分布, MCMC模拟基本步骤如下:
(1) 确定待识别的模型参数θ及其先验边缘分布;
(2) 将式(3)作为似然函数, ∑为对角矩阵, 利用观测数据y, 通过DREAMzs抽样得到参数后验样本{θi}(i=1, …, N), 根据θi和模型预测点输入向量x*, 分别运行地下水模型, 获得模型预测输出的后验样本yi*=Mi*; DREAMzs抽样算法细节详见文[15];
(3) 统计分析yi*, 得到模型预测均值y*及置信水平为α下预测区间
1.2 基于高斯回归的模型结构不确定性分析
对于考虑结构误差的模型, 在式(1)上引入了结构误差项, 将结构误差与测量误差分开处理[26]:
(4) 式中: b—结构误差;
ε—测量误差;
Φ—高斯回归超参数。
高斯过程回归(GPR)[27]是一种非参数贝叶斯核函数回归方法, 该方法能够对误差进行统计学习。在高斯过程回归中, 随机变量b(x, Φ)服从多元高斯分布即b(x, Φ)~N (μ, C), μ为均值函数, C为协方差函数。本文均值函数μ=0, 协方差函数采用平方指数型:
(5) 式中: n—观测数据的个数;
Ι—指示函数, 若i=j, 则Ι=1, 否则Ι=0;
Φ—超参数;
λ—特征长度的超参;
假设测量误差独立同分布, 即
(6) 式(6)中, 右侧第一项代表模型输出对观测数据的拟合效果, 第二项代表对模型M的复杂度惩罚, 第三项为标准化常数。
利用GPR进行模型结构误差统计学习时, 需要同时识别模型参数θ与超参数Φ。假设θ与Φ相对独立, 根据贝叶斯原理, 通过观测数据y, 推导出参数θ与Φ的后验分布, 即
(7) 其中, p(y|θ, Φ)为似然值, 可由式(6)求得; p(θ, Φ|y)为后验分布; p(θ)为θ先验分布; p(Φ)为Φ先验分布。由于参数后验p(θ, Φ|y)难以直接求得, 本文使用DREAMzs算法结合GPR识别θ, Φ的后验分布。
识别出θ, Φ后验分布之后, 可以对结构误差进行模拟预测。由于y-M与b*先验联合分布服从多元正态分布, 即:
(8) 在已有训练数据的条件下, 得到b*的后验分布:
(9) (10) (11) 式中: b*预测点结构误差后验均值;
μ*—预测点结构误差的先验均值;
C*、C**—先验协方差矩阵;
Cbb(b*)—后验协方差矩阵。
进行多元正态随机抽样得到b*、ε*, 可得模型模拟预测值:
(12) 式中: x*—模型预测输入向量(即预测点);
b*—预测点结构误差;
ε*—预测点观测误差;
M*—预测点模型输出值;
y*—预测值。
综上, 结合GPR进行模型结构不确定性分析的基本步骤如下:
(1) 确定待识别的模型参数θ与超参数Φ及其先验边缘分布;
(2) 将式(6)作为似然函数, 利用观测数据y, 通过DREAMzs抽样得到参数后验样本{θi, Φi}(i=1, …, N), 根据θi、Φi及模型观测与预测输入向量x、x*, 运行地下水模型, 分别得到
(3) 基于步骤(2), 根据式(8)~(11), 采用多元正态抽样得到
(4) 统计分析
2. 海水入侵数值模拟算例分析
针对理想条件下的岩溶裂隙介质海水入侵问题, 利用简化模型结构的地下水模型描述海水入侵过程时, 分别进行考虑和不考虑模型结构误差的海水入侵预测不确定性分析, 验证基于高斯回归方法模型结构不确定性分析的可靠性。
2.1 海水入侵模型概况
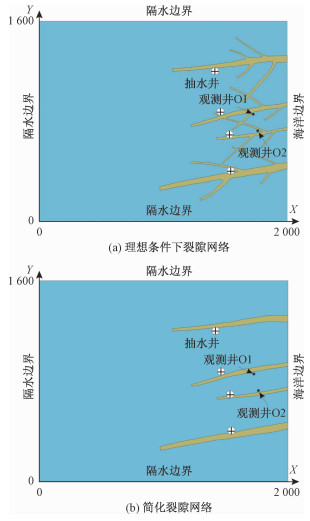
本文建立一个理想条件下三维岩溶裂隙介质海水入侵模型, 模型裂隙结构见图 1(a)。研究区在平面上为一个矩形, 长2 000 m, 宽1 600 m, 垂向上厚度为40 m。裂隙网络包括4条主裂隙和若干次级裂隙。采用等效多孔介质方法对该区域进行概化, 裂隙区水平渗透系数为50 m/d, 纵向弥散度为30 m, 孔隙度为0.2, 非裂隙区水平渗透系数为5 m/d, 纵向弥散度为10 m, 孔隙度为0.1, 垂直水平渗透系数之比为0.1, 横纵弥散度比为0.1。模型东侧为海洋边界即定水头H=0 m与定浓度边界C=20 g/L, 南、北、西边界为隔水边界。研究区内共有4口抽水井, 流量均为350 m3/d, 两个观测井。研究区表面均匀接受降水补给, 降水入渗系数为0.001 m/d。初始流场为抽水前稳定状态下的地下水流场。利用三维、变密度海水入侵数值模拟程序-SEAWAT4[28]建立数值模型, 模拟期设为1 600 d。将观测井处的模拟浓度加上高斯白噪声观测误差(均值为0, 方差为1)作为本次算例分析的观测数据。
考虑实际场地条件下的岩溶裂隙分布复杂, 难以对其空间分布进行准确刻画, 通常对裂隙网络进行简化处理, 从而导致模型结构误差。如图 1(b)所示, 假设野外勘察工作仅识别出4条主裂隙, 而忽略了次级裂隙分布。基于该简化的模型结构来描述海水入侵过程时, 模拟结果将会受到模型结构和模型参数不确定性的影响。
2.2 海水入侵数值模拟不确定性分析
针对简化模型结构的地下水模型, 分别在考虑和不考虑模型结构误差的条件下, 进行海水入侵数值模拟的不确定性分析。假设地下水模型中的非裂隙区渗透系数K1、弥散度α1、裂隙区渗透系数K2、弥散度α2为未知参数, 而模型边界条件、初始条件、模型其它参数和源汇项与真实模型相同。模型识别期为0~1 300 d, 模型验证期为1 301~1 600 d。4个未知模型参数(K1、K2、α1、α2)和3个高斯回归超参数(σs、λ、σε)的先验分布, 见表 1。其中, 对于特征长度λ, 基于Brynjarsdóttir与O’Hagan的经验[29], 其先验分布为Gamma分布, 且特征长度λ过小将会降低模型预测能力, λ过大则难以学习到误差的统计特征, 因此需要对λ进行限制[27]。此外, 本次研究采用DREAMzs算法识别未知的模型参数(包括统计模型参数)时, 设置4条平行的马尔科夫链。
表 1 模型参数的边缘先验分布与地下水模型参数真实值Table 1. Prior distributions of model parameters and true values of groundwater model parameters
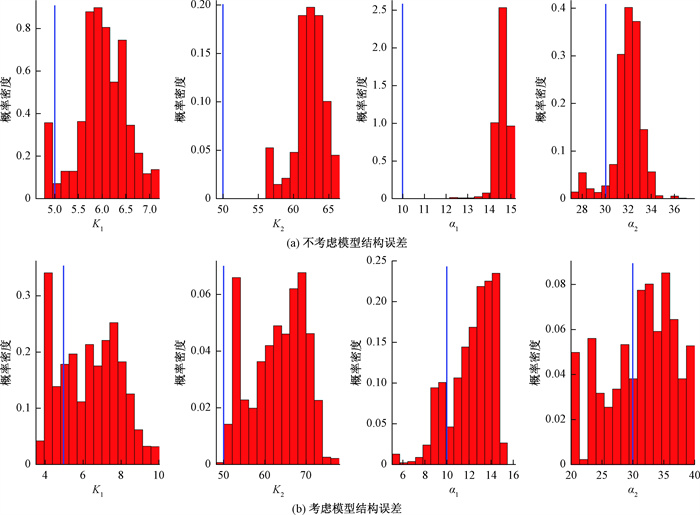
不考虑结构误差时, MCMC单链运行510次达到收敛, 取收敛后的8 000次样本统计其参数边缘后验分布, 见图 2(a)。
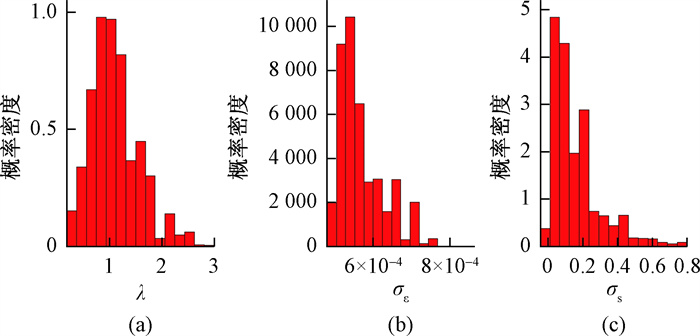
考虑结构误差时, MCMC单链运行1 220次达到收敛, 取收敛后的8 000次样本统计其参数边缘后验分布, 如图 2(b)、图 3所示。
由图 2可以看出, 对于参数K1, 考虑结构误差时得到的K1边缘后验分布在真实值处具有较大的预测概率, 且考虑结构误差时K1真值更加靠近后验分布峰值; 对于参数K2, 不考虑结构误差时边缘后验分布不能包含K2真值, 而考虑结构误差后K2真值落在边缘后验分布内; 对于参数α1, 不考虑结构误差时边缘后验分布同样不能包含α1的真值, 但考虑结构误差时α1的真值落在边缘后验分布内, 且较靠近峰值; 对于参数α2, 考虑与不考虑结构误差时, 后验分布均包含α2真值, 但考虑结构误差时在真实值处具有更大的预测概率, 且峰值更加靠近真实值。因此, 基于高斯过程结构误差驱动模型显著降低了参数K1、K2、α1、α2补偿模型结构误差的程度。
基于MCMC得到的参数后验分布样本, 获得相对应的模型模拟结果, 通过频率统计可得到模拟值(或预测值)的置信区间与平均值等, 如将95%水平下的置信区间(2.5%~97.5%)作为本次研究的预测区间。使用预测区间覆盖率(即观测数据位于预测区间的比例), ME值(即观测值与预测值之差的均值)和RMSE值(即观测值与预测值之差的均方根)来表征模型的预测性能。预测区间包含率越高, ME值的绝对值越小, RMSE值越小, 预测值越靠近观测值, 表示预测性能越好。在考虑和不考虑结构误差情况下的各指标的统计分析见表 2。
表 2 模型预测性能指标统计Table 2. Statistics of model prediction performance indicators
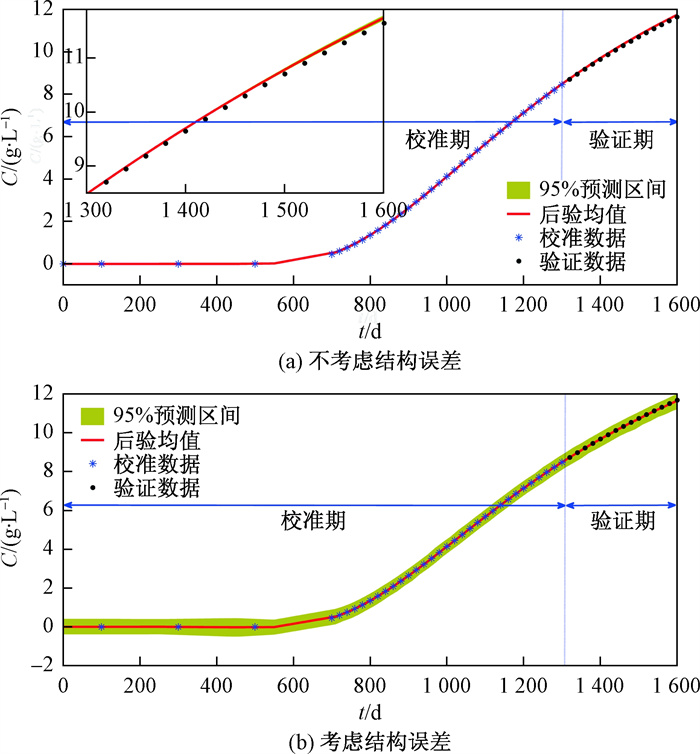
如图 4所示, 分别为在不考虑和考虑结构误差条件下的O1观测井浓度预测曲线, 可以发现考虑结构误差之后, 预测区间明显变宽。根据对模型预测性能的定量评价指标(表 2), 可以发现, 在模型识别期, 考虑模型结构误差之后, 模型预测ME绝对值和RMSE值均显著降低, 预测区间覆盖率有所提升(由42.9%提升至100%)。在模型验证期, 考虑模型结构误差之后, 模型预测ME绝对值和RMSE值均有所降低, 预测区间覆盖率显著提升(由0提升至100%)。因此, 通过考虑模型结构误差, 能够提高模型预测能力。
3. 溶质运移柱体实验数值模拟算例分析
本文以LV等[30]一维溶质运移柱体实验为例, 建立溶质运移数值模型, 分别在考虑结构误差与不考虑结构误差的条件下, 对水文地质参数进行反演并进行不确定性分析。
3.1 溶质运移实验概况
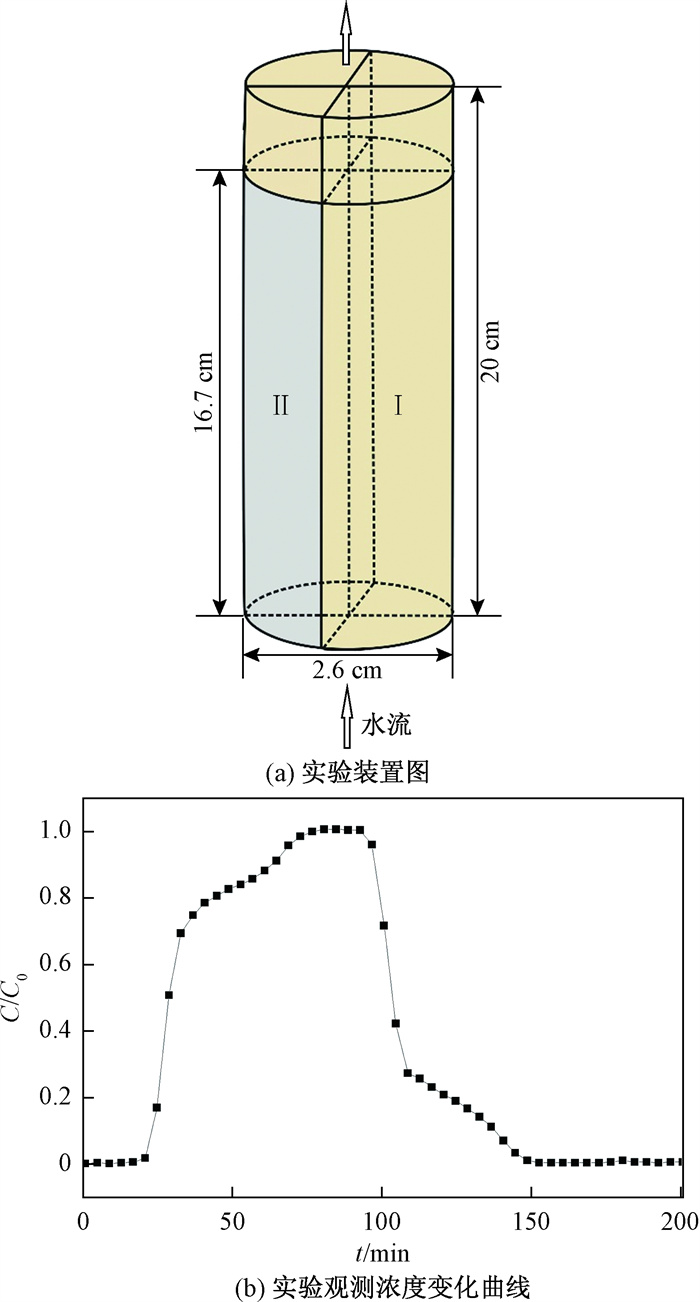
图 5(a)为该实验装置图, 装置为圆形砂柱, 直径2.6 cm, 砂柱高20.0 cm, 砂柱由两部分组成: RegionI直径为920 μm的石英砂均匀填充, RegionⅡ由直径为550 μm的石英砂均匀填充。实验开始前75.4 min, 以1 mL/min的流速从砂柱下端注入浓度为C0的KNO3溶液, 之后以1 mL/min的流速通入纯净水。从注入KNO3时开始计时, 每隔4 min检测上端流出溶液浓度C, 并得到相对浓度C/C0。在图 5(a)装置条件下, 共得到71个时刻(即第1、4、…、281 min时刻)的KNO3的相对浓度, 以此作为观测值, 得到相对浓度观测曲线(图 5b)。
3.2 溶质运移数值模拟不确定性分析
对上述KNO3运移实验过程进行概化, 利用ModFlow2005[31]和MT3DMS[32]分别建立地下水流模型和溶质运移模型。模型在平面上剖分为24×24个格栅, 模型垂向上剖分为40层。假设地下水模型中RegionI渗透系数K1、纵向弥散度α1和RegionⅡ渗透系数K2、纵向弥散度为α2为未知参数。模型圆柱的内壁设为隔水边界, 上下底部均设为定流量边界。此外, 整个实验柱体孔隙度设为0.33、横向弥散度与纵向弥散度之比取0.1。
考虑到实际溶质运移过程的复杂性, 难以对含水层结构进行精细刻画, 未考虑吸附化学反应等过程及常规对流弥散方程的缺陷[33], 从而产生结构误差。利用概化的模型模拟溶质过程时, 模拟结果将会受到模型结构和模型参数不确定性的影响。
分别在考虑和不考虑模型结构误差的条件下, 进行柱体实验溶质运移数值模拟的不确定性分析。模型识别期为0~117 min, 模型验证期为118~201 min。表 3所示为4个未知模型参数(K1、K2、α1、α2)和3个高斯回归超参数(σs、λ、σε)的先验分布。本次研究采用DREAMzs算法识别未知的模型参数(包括统计模型参数), 设置4条平行的马尔科夫链。
表 3 模型参数的边缘先验分布Table 3. Marginal prior distributions of model parameters
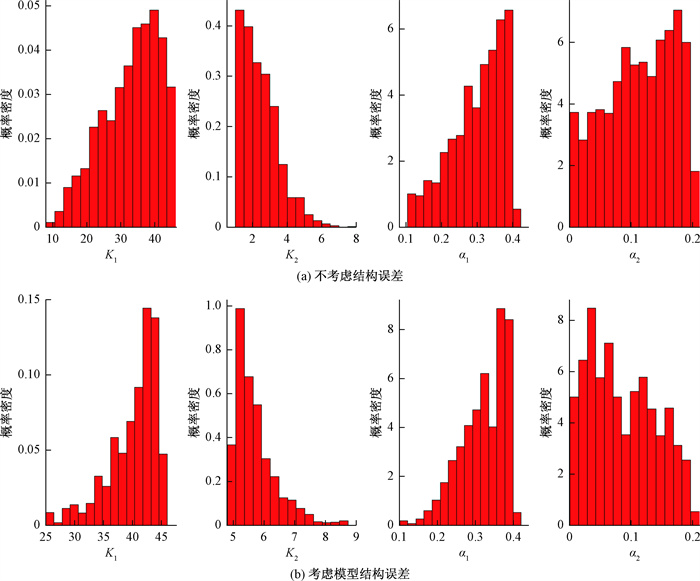
不考虑结构误差时, MCMC单链运行260次达到收敛, 取收敛后的8 000次样本统计其参数边缘后验分布, 如图 6(a)所示。
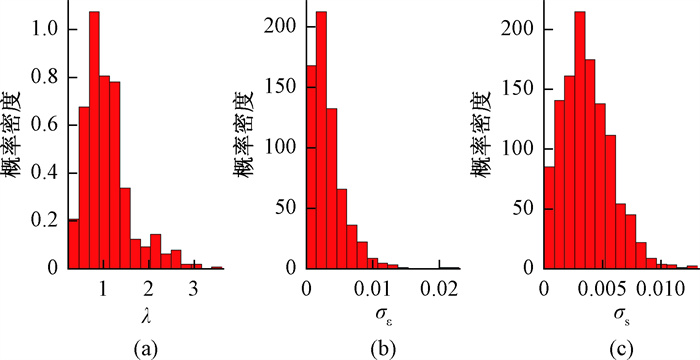
考虑结构误差时, MCMC单链运行990次达到收敛, 取收敛后的8 000次样本统计其参数边缘后验分布(图 6b、图 7)。
对于真实的地下水模型, 模型参数的真值未知, 因此无法验证参数后验分布的正确性。对比图 6(a)、(b), 可以看出两种方法得到的参数边缘后验分布有一定的重合, 但是对于参数K1与K2, 考虑结构误差时参数边缘后验分布的范围及峰态与不考虑结构误差相比存在较大的差异。同时对于参数α1与α2, 两种方法得到的参数后验分布的峰态也存在差异。这表明, 是否考虑结构误差, 会导致模型参数识别的差异。
基于MCMC得到的参数后验分布样本, 计算相对应的模型模拟结果, 通过频率统计可得的模拟值的95%置信区间(即预测区间)与平均值(即预测值)。对预测区间覆盖率, ME值和RMSE值进行统计分析, 见表 4。
表 4 模型预测性能指标统计Table 4. Statistics of model prediction performance indicators
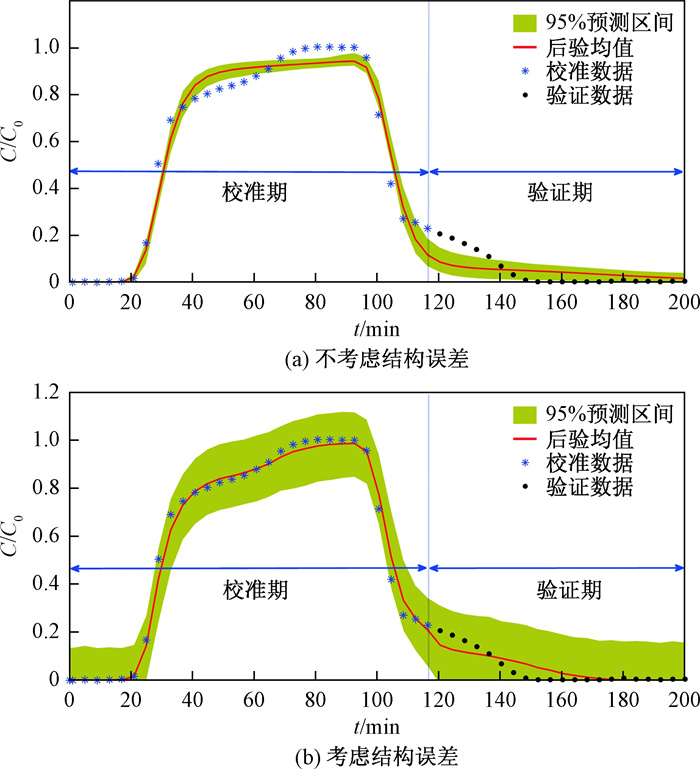
在不考虑和考虑结构误差条件下实验柱体端口处平均浓度的穿透曲线, 如图 8所示。可以看出, 考虑结构误差条件下, 预测区间覆盖区域更大。结合模型预测性能的定量评价指标(表 4), 可以发现, 在模型识别期, 考虑模型结构误差之后, 模型预测ME绝对值和RMSE值均明显降低, 预测区间覆盖率显著提升(由33.3%提升至100%)。在模型验证期, 考虑模型结构误差之后, 模型预测ME绝对值和RMSE值均有所降低, 预测区间覆盖率也有所提升(由42.9%提升至100%)。因此, 考虑模型结构误差之后, 模型预测值更加接近观测值, 模型具有更好的预测性能。
4. 结论及展望
地下水模型结构受到地层岩性、地质构造、化学反应过程等多种不确定因素的影响。但囿于人类认知与勘测资料, 这些不确定性因素无法避免, 因此存在模型系统偏差。本次研究提出一种基于高斯过程回归(GPR)的模型结构不确定性分析方法。该方法利用GPR对模型结构误差进行统计学习, 并将DREAMzs算法与GPR算法相结合, 有效提高了地下水数值模拟及预测结果的可靠性。
基于两个案例分析-理想岩溶裂隙区海水入侵模型与室内溶质运移柱体实验, 通过对比在考虑与不考虑结构误差的条件下, 获得的参数边缘后验分布及预测分布区间。结果发现: 考虑模型结构误差之后, 模型参数边缘后验分布更加靠近真实值, 在参数识别过程减轻了参数补偿的影响, 同时模型预测区间对观测数据的包含率显著变大, 预测结果的平均误差(ME)绝对值与均方根误差(RMSE)值也明显降低, 模型具有更好的预测性能。因此, 通过数据驱动模型考虑结构误差, 可以减轻参数识别过程中的参数补偿, 提高模型的模拟及预测性能。
在观测数据有限的条件下, 考虑结构误差的数据驱动模型方法会导致预测区间宽度一定程度的增加, 通过融合其他类型的观测数据, 可进一步降低模型预测不确定性。
-
表 1 模型参数的边缘先验分布与地下水模型参数真实值
Table 1 Prior distributions of model parameters and true values of groundwater model parameters

表 2 模型预测性能指标统计
Table 2 Statistics of model prediction performance indicators

表 3 模型参数的边缘先验分布
Table 3 Marginal prior distributions of model parameters

表 4 模型预测性能指标统计
Table 4 Statistics of model prediction performance indicators

-
[1] DUMEDAH G, WALKER J P. Assessment of model behavior and acceptable forcing data uncertainty in the context of land surface soil moisture estimation[J]. Advances in Water Resources, 2017, 101: 23-36. DOI: 10.1016/j.advwatres.2017.01.001
[2] 吴吉春, 陆乐. 地下水模拟不确定性分析[J]. 南京大学学报(自然科学版), 2011, 47(3): 227-234. WU J C, LU L. Uncertainty analysis for groundwater modeling[J]. Journal of Nanjing University(Natural Sciences), 2011, 47(3): 227-234. (in Chinese)
[3] WATSON T A, DOHERTY J E, CHRISTENSEN S. Parameter and predictive outcomes of model simplification[J]. Water Resources Research, 2013, 49(7): 3952-3977. DOI: 10.1002/wrcr.20145
[4] WU J C, ZENG X K. Review of the uncertainty analysis of groundwater numerical simulation[J]. Chinese Science Bulletin, 2013, 58(25): 3044-3052. DOI: 10.1007/s11434-013-5950-8
[5] 束龙仓, 朱元生. 地下水资源评价中的不确定性因素分析[J]. 水文地质工程地质, 2000, 27(6): 6-8. DOI: 10.3969/j.issn.1000-3665.2000.06.002 SHU L C, ZHU Y S. Analysis of uncertainties in groundwater resource evaluation[J]. Hydrogeology & Engineering Geology, 2000, 27(6): 6-8. (in Chinese) DOI: 10.3969/j.issn.1000-3665.2000.06.002
[6] 束龙仓, 陶玉飞, 刘佩贵. 考虑水文地质参数不确定性的地下水补给量可靠度计算[J]. 水利学报, 2008, 39(3): 346-350. SHU L C, TAO Y F, LIU P G. Reliability calculation method for groundwater recharge in consideration of uncertainty of hydrogeological parameters[J]. Journal of Hydraulic Engineering, 2008, 39(3): 346-350. (in Chinese)
[7] KUNSTMANN H, KINZELBACH W, SIEGFRIED T. Conditional first-order second-moment method and its application to the quantification of uncertainty in groundwater modeling[J]. Water Resources Research, 2002, 38(4): 1-6.
[8] DETTINGER M D, WILSON J L. First order analysis of uncertainty in numerical models of groundwater flow part: 1. Mathematical development[J]. Water Resources Research, 1981, 17(1): 149-161. DOI: 10.1029/WR017i001p00149
[9] 于勇, 翟远征, 郭永丽, 等. 基于不确定性的地下水污染风险评价研究进展[J]. 水文地质工程地质, 2013, 40(1): 115-123. YU Y, ZHAI Y Z, GUO Y L, et al. Risk assessment of groundwater pollution based on uncertainty[J]. Hydrogeology & Engineering Geology, 2013, 40(1): 115-123. (in Chinese)
[10] BEVEN K, BINLEY A. The future of distributed models-model calibration and uncertainty prediction[J]. Hydrological Processes, 1992, 6(3): 279-298. DOI: 10.1002/hyp.3360060305
[11] HASSAN A E, BEKHIT H M, CHAPMAN J B. Using Markov Chain Monte Carlo to quantify parameter uncertainty and its effect on predictions of a groundwater flow model[J]. Environmental Modelling & Software, 2009, 24(6): 749-763.
[12] HASSAN A E, BEKHIT H M, CHAPMAN J B. Uncertainty assessment of a stochastic groundwater flow model using GLUE analysis[J]. Journal of Hydrology, 2008, 362(1): 89-109.
[13] 陆乐, 吴吉春, 陈景雅. 基于贝叶斯方法的水文地质参数识别[J]. 水文地质工程地质, 2008, 35(5): 58-63. DOI: 10.3969/j.issn.1000-3665.2008.05.014 LU L, WU J C, CHEN J Y. Identification of hydrogeological parameters based on the Bayesian method[J]. Hydrogeology & Engineering Geology, 2008, 35(5): 58-63. (in Chinese) DOI: 10.3969/j.issn.1000-3665.2008.05.014
[14] VRUGT J A, BRAAK C J F T, DIKS C G H, et al. Accelerating Markov Chain Monte Carlo simulation by differential evolution with self-adaptive randomized subspace sampling[J]. International Journal of Nonlinear Sciences & Numerical Simulation, 2011, 10(3): 273-290.
[15] LALOY E, VRUGT J A. High-dimensional posterior exploration of hydrologic models using multiple-try DREAM(ZS)and high-performance computing[J]. Water Resources Research, 2012, 50(3): 182-205.
[16] SADEGH M, VRUGT J A. Approximate Bayesian Computation using Markov Chain Monte Carlo simulation: DREAM(ABC)[J]. Water Resources Research, 2015, 50(8): 6767-6787.
[17] ERDAL D, NEUWEILER I, HUISMAN J A. Estimating effective model parameters for heterogeneous unsaturated flow using error models for bias correction[J]. Water Resources Research, 2012, 48(48): 2061-2066.
[18] DOHERTY J, WELTER D. A short exploration of structural noise. [J]. Water Resources Research, 2010, 46(5): W5525. http://www.cabdirect.org/abstracts/20103245945.html
[19] NEUMAN S P. Maximum likelihood Bayesian averaging of uncertain model predictions[J]. Stochastic Environmental Research & Risk Assessment, 2003, 17(5): 291-305.
[20] ROJAS R, FEYEN L, DASSARGUES A. Conceptual model uncertainty in groundwater modeling: Combining generalized likelihood uncertainty estimation and Bayesian model averaging[J]. Water Resources Research, 2008, 44(12): W12418.
[21] PARRISH M A, MORADKHANI H, DECHANT C M. Toward reduction of model uncertainty: Integration of Bayesian model averaging and data assimilation[J]. Water Resources Research, 2012, 48(3): 3519.
[22] DEMISSIE Y K, VALOCCHI A J, MINSKER B S, et al. Integrating a calibrated groundwater flow model with error-correcting data-driven models to improve predictions[J]. Journal of Hydrology, 2009, 364(3): 257-271.
[23] XU T F, VALOCCHI A J. A Bayesian approach to improved calibration and prediction of groundwater models with structural error[J]. Water Resources Research, 2015, 51(11): 9290-9311. DOI: 10.1002/2015WR017912
[24] XU T F, VALOCCHI A J, YE M, et al. Quantifying model structural error: Efficient Bayesian calibration of a regional groundwater flow model using surrogates and a data-driven error model[J]. Water Resources Research, 2017, 53(5): 4084-4105. DOI: 10.1002/2016WR019831
[25] CARRERA J, NEUMAN S P. Estimation of aquifer parameters under transient and steady state conditions: 1. maximum likelihood method incorporating prior information[J]. Water Resources Research, 1986, 22(2): 199-210. DOI: 10.1029/WR022i002p00199
[26] KENNEDY M C, O'HAGAN A. Bayesian calibration of computer models[J]. Journal of the Royal Statistical Society: Series B Statistical Methodology, 2001, 63(3): 425-464. DOI: 10.1111/1467-9868.00294
[27] RASMUSSEN C, WILLIAMS C. Gaussian processes for machine learning[M]. Cambridge: MIT Press, 2006: 69-106.
[28] LANGEVIN C D, THORNE J R D T, DAUSMAN A M, et al. SEAWAT version 4: A computer program for simulation of multi-species solute and heat transport[R]. Reston, Virginia: US Geological Survey, 2008.
[29] BRYNJARSDTTIR J, O'HAGAN A. Learning about physical parameters: the importance of model discrepancy[J]. Inverse Problems, 2014, 30(11): .
[30] LV X, GAO B, SUN Y, et al. Effects of grain size and structural heterogeneity on the transport and retention of nano-TiO2 in saturated porous media[J]. Science of The Total Environment, 2016, 563/564: 987-995.
[31] HARBAUGH A W. MODFLOW-2005, the US Geological Survey modular groundwater model-the groundwater flow process[R]. Reston: US Geological Survey, 2005.
[32] ZHENG C, WANG P P. MT3DMS: A modular Three-Dimensional multispecies transport model for simulation of advection, dispersion and chemical reactions of contaminants in groundwater systems[R]. Vicksburg, Mississippi: US Army Engineer Research and Development Center, 1999.
[33] BENSON D A, SCHUMER R, MEERSCHAERT M M, et al. Fractional dispersion, Lévy Motion, and the MADE tracer tests[J]. Transport in Porous Media, 2001, 42(1/2): 211-240.
-
期刊类型引用(8)
1. 南天,曹文庚,任印国,孙龙,高媛媛. 京津冀平原浅层地下水漏斗演变规律与影响因素. 南水北调与水利科技(中英文). 2024(01): 110-121 .  百度学术
百度学术
2. 夏传安,樊秀峰,王浩,简文彬. 耦合变密度地下水流降阶模型与高斯过程的蒙特卡罗模拟. 水文地质工程地质. 2024(05): 1-13 .  本站查看
本站查看
3. 董贵明,王颖,詹红兵,田娟,李嘉宁,代丽娜. 二维承压非稳定流水均衡区间的数值模拟. 地质科技通报. 2023(04): 75-82 .  百度学术
百度学术
4. 杨运,吴吉春,骆乾坤,钱家忠. 考虑预报偏差的迭代式集合卡尔曼滤波在地下水水流数据同化中的应用. 水文地质工程地质. 2022(06): 13-23 .  本站查看
本站查看
5. 高烨,梁收运,王申宁,刘富强,张洪伟. 地下水数值模拟不确定性分析研究进展. 地下水. 2020(01): 28-31+97 .  百度学术
百度学术
6. 赵洁,林锦,吴剑锋,吴吉春. 未来气候变化对大连周水子地区海水入侵程度的影响预测. 水文地质工程地质. 2020(03): 17-24 .  本站查看
本站查看
7. 李选彧. 未来气候变化对丹东市海水入侵程度的影响预测. 黑龙江水利科技. 2020(10): 59-64 .  百度学术
百度学术
8. 张琛,段磊,刘明明,李瑛,宋浩. 伊犁河支流大西沟河水与地下水转化关系研究. 水文地质工程地质. 2019(03): 18-26 .  本站查看
本站查看
其他类型引用(10)




 下载:
下载:
 邮件订阅
邮件订阅 RSS
RSS