在我国西南地区, 多重岩溶含水介质常由基岩裂隙和岩溶管道构成, 水动力场非常复杂^[1], 传统的地下水数值模拟难以刻画岩溶地下水流特征^[2-3]。Shoemaker等在MODFLOW-2005开源程序的基础上增加管道流程序(Conduit Flow Process, CFP), 分别应用Hagen-Poiseuille方程和Darcy-Weisbach方程描述岩溶管道介质中层流和紊流运动^[4-5]。CFP能够刻画岩溶管道特征和快速的优先流, 适用于复杂的多重岩溶含水介质。许多学者运用理想模型对CFP性能进行测试: Hill等^[6]通过对比传统等效多孔介质模型和管道流CFP模型(双重介质), 基于观测和模拟流量结果比较, 得出的管道流程序模拟更加精确; Gallegos等^[7]基于物理沙箱模型和Woodville岩溶区观测数据, 运用CFP模拟泉水流量, 得出管道流程序能够模拟岩溶泉流量动态特征; Giese等^[8]应用CFP模型研究管道中水流的紊流运动特征; 常勇^[9]基于MODFLOW-CFP模型模拟岩溶含水层内管道-裂隙二元结构水文过程, 并提出一种新的水箱——CFP组合模型; 焦友军等^10]采用CFP模型模拟岩溶含水系统在暴雨期的响应过程。

CFP模型也可用于研究溶质运移特征。Faulkner等^[11]利用实验室物理模型和数值模型研究基岩裂隙和岩溶管道双重介质溶质运移特征和交换规律, 将岩溶含水层分为两个区域(基岩裂隙和岩溶管道区), 地下水在基岩裂隙区符合达西定律, 而在岩溶管道内满足Navier-Stokes方程, 数值模拟的水头分布、流量和溶质运移特征与物理实验结果一致。Ghasemizadeh等^[12]对岩溶区等效介质、裂隙介质及管道介质水流模型和溶质运移模型进行总结。等效介质和裂隙介质模型所需数据少, 概化岩溶介质内部结构特征建模方便, 但不能刻画水量和水质的空间分布特征; 等效介质模型不适应于岩溶区, 而在等效介质基础上耦合分布式管道(CFP)模型能够模拟管道-裂隙介质水流系统, 但对模型数据和参数需求较高。模块化三维溶质迁移模型(The modular three-dimentional transport model, MT3DMS), 是国际上应用最广的地下水系统污染物迁移模拟程序^[13-15]。基于岩溶管道流程序研究岩溶管道裂隙水流运动较为成熟^[16-18], 但结合污染物在管道中的运移特征研究相对较少。

本文的目的是以概念模型为例, 通过耦合CFP和MT3DMS研究岩溶管道流溶质运移特征, 并讨论管道参数如管道直径、水力梯度及水流交换系数对溶质运移模拟结果的影响, 以期更好地理解实际岩溶区溶质运移现象。

1.   研究方法

1.1   管道流模型(CFP)

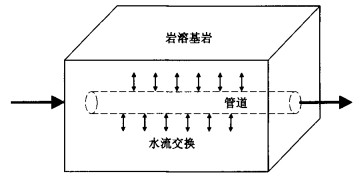
CFP模型是在孔隙介质层流模型(MODFLOW-2005)基础上耦合离散的管道网络, 符合西南岩溶区双重介质水流系统^[19-20](图 1)。

图  1  CFP原理示意图

Figure  1.  Schematic diagram showing the principle of CFP

下载: 全尺寸图片 幻灯片

孔隙介质层流模型基于单元中心有限差分法, 层流模型地下水在三维空间的流动符合达西定律, 公式如下:

式中: K_xx、K_yy、K_zz——渗透系数在x、y、z方向上的分量/(m·d^-1);

h——水头/m;

W——单位体积流量, 代表流进汇和来自源的水量/d^-1;

S_s——孔隙介质的贮水率/m^-1;

t——时间/d。

式(1)假设地下水流无黏性, 密度不变, 不可压缩且属于达西流。渗透系数的主轴方向与坐标轴方向一致。加上相应的初始条件和边界条件, 构成地下水流孔隙介质数学模型。MODFLOW-2005提供多种数值方法求解线性及非线性给定水头边界、给定流量边界及第三类边界条件。

管道系统是由节点和圆柱形管道组成, 可参考Shoemaker等发表的CFP使用手册。根据体积守恒定律, 每一个节点水流状态可应用Kirchhoff定律描述(式2)。当管道水流处于层流状态时, 应用Hagen-Poiseuille(式3)描述; 管道水流处于紊流状态时, 应用Darcy-Weisbach(式4)描述, CFP应用式(5)计算管道与岩溶基岩水流交换。

式中: Q_ip——从管道i到管道n的流量/(m³·d^-1);

Q_ss——所有节点源汇项流量总和/(m³·d^-1);

d——管道直径/m;

g——重力加速度/(m·d^-2);

Δh_c——管道水头损失/m;

υ——水动力黏滞系数/(m²·d^-1);

Δl——管道长度/m;

k_c——管道平均粗糙度, 与管道壁形态有关;

Q_ex——管道与基岩交换水量/(m³·d^-1), 值为负表示水流从基岩流向岩溶管道, 值为正表示水流从管道流向基岩含水层;

α_ex——管道渗透系数/(m²·d^-1);

h_c——管道内水头/m;

h_m——基岩水头/m。

1.2   模块化三维溶质迁移模型(MT3DMS)

MT3DMS是国际上应用最广的地下水系统污染物迁移模拟程序(对流、弥散及生化反应等), 该模型能够灵活有效地处理各种源汇项和边界条件, 适用于承压、无压及承压-无压含水层中的污染物运移问题。偏微分式(6)用于描述污染物k在三维非稳定流系统中的溶质运移特性。

式中: R——阻滞因子, 无量纲;

θ——含水介质孔隙度, 无量纲;

C^k——水中的污染物k的浓度/(kg·m^-3);

t——时间/d;

x_i、x_j——空间坐标/m;

D_ij——水动力弥散系数张量/(m²·d^-1);

v_i——地下水渗透流速/(m·d^-1);

q_s——源(正值)或汇(负值)的单位流量/d^-1;

$C_{\mathrm{s}}^k$——污染物k的源或汇的浓度/(kg·m^-3);

$\sum R_n$——化学反应项/(kg·m^-3·d^-1)。

MT3DMS采用模块化的结构子程序包来实现不同功能。不包括求解地下水流方程的子程序, 通过任何块中心有限差分水流模型的输出结果来获得地下水位资料, 如MODFLOW等。其中子程序包主要包括基本运移子程序包(BTN)、水流模型接口包(FMI)、对流子程序包(ADV)、弥散子程序包(DSP)、源汇项子程序包(SSM)、化学反应子程序包(RCT)、GCG迭代求解程序包(GCG)及实用工具子程序包(UTL)。

2.   概念模型

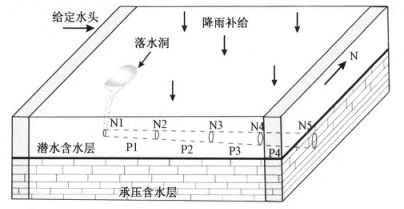
管道流CFP中概念模型分为两层, 含水层由基岩网格和管道组成。第一层表示潜水含水层, 第二层表示承压含水层, 管道设置在第二层, 每层厚20 m(图 2)。网格大小10 m×10 m, 共计47列, 31行。水平渗透系数为1 m/h, 垂向各向异性比为10, 潜水含水层给水度为0.1, 承压含水层储水系数为0.000 1。模型第1列和第47列为给定水头边界, 其余为零通量边界。其中管道P1至管道P4, 管道直径分别为0.2 m、0.3 m、0.4 m和0.5 m, 弯曲度为1, 管道粗糙度为0.001, 下临界雷诺数为2 000, 上临界雷诺数为4 000。节点N1至节点N5渗透系数α_ex为0.1 m²/h。

图  2  管道流CFP概念模型

Figure  2.  Conceptual model for CFP

下载: 全尺寸图片 幻灯片

应力期分为8个, 暴雨期前10 h平水期为第一应力期, 第二至第七应力期暴雨期间隔4 h, 暴雨后持续模拟686 h, 共计30 d, 落水洞处N1节点为集中降雨补给, 其余为地表降水面状补给。在没有降雨情况下, 第二层含水介质等水位线图如图 3所示, 其中第1、47列为给定水头边界, 水流自左向右流动, 等水位线在管道处有突变。由于水力梯度大, 管道处于承压状态, 雷诺数最小为37 047, 水流为紊流状态。

图  3  岩溶含水层第二层等水位线图

Figure  3.  Contours of groundwater level in the 2^th layer of the karst aquifer

下载: 全尺寸图片 幻灯片

从表 1可以看出, 在模型末期, 节点N1、N2、N3、N4处管道水头低于周围基岩含水层水头(N5为给定水头), 水流从周围含水层向管道径流, 管道为承压状态, 其中节点N1接受含水层补给为187.10 m³/h, 并流向管道P1;节点N2接受含水层补给296.29 m³/h, 管道P1补给187.10 m³/h, 并流向管道P2;节点N3接受含水层补给224.39 m³/h, 管道P2补给483.39 m³/h, 并流向管道P3;节点N4接受含水层补给124.24 m³/h, 管道P3补给707.78 m³/h, 并流向管道P4, 节点N5流出量为832.02 m³/h, 满足守恒定律(式5)。在此水流模型基础上运行MT3DMS模型, 为模拟岩溶区示踪试验, 仅在落水洞处第一应力期示踪剂浓度为100 mg/L, 其余初始浓度为0。不考虑化学反应情况下, 选择对流、弥散及源汇项子程序包。孔隙度为0.1, 纵向弥散度为100 m, 横向弥散度为10 m, 垂向弥散度为1 m。Field计算出岩溶地区弥散系数介于0.08~1 m²/s^[21], 而在实际工作中, 通过示踪试验计算岩溶管道内流速介于0.002~1.121 m/s(计算管道平均直径和出口流量), 弥散度介于1~500 m之间, 因此弥散度设置为100 m是合理的。

表  1  模拟末期水流交换特征

Table  1.  Characteristics of water exchange between conduit and matrix

下载: 导出CSV 

| 显示表格

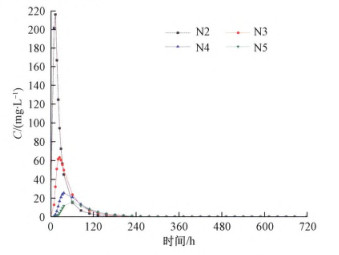
分别对比模拟N2至出口N5处浓度运移曲线(图 4), N2、N3、N4、N5处距离投放点距离分别为100, 200, 300, 400 m。从图 4中可以看出, 管道中溶质运移存在明显拖尾现象, 且距离越长拖尾越明显; 距离越短峰值浓度越大, 到达峰值的时间越短, 符合实际岩溶区示踪试验穿透曲线。

图  4  不同距离接收点浓度曲线

Figure  4.  Concentration curves at different distances

下载: 全尺寸图片 幻灯片

3.   讨论

为研究不同水文地质参数对溶质运移的影响, 选取管道P3中点距离投放点250 m处为研究对象, 探讨孔隙度、弥散系数、水力梯度、管道直径和管道渗透系数对溶质穿透曲线的影响。由于岩溶区浓度穿透曲线存在拖尾现象, 为评估曲线的拖尾情况, 引入偏态系数SK, 该参数是研究曲线不对称程度的统计参数(式7)。当偏态系数为0时, 表示浓度穿透曲线完全对称分布; 当偏态系数大于0时, 表示浓度穿透曲线为正偏态; 当偏态系数小于0时, 表示浓度穿透曲线为负偏态。

式中: SK——偏态系数;

C_i——第i个浓度值/(kg·m^-3);

$\overline{C}$——浓度平均值/(kg·m^-3);

σ——均方差;

N——个数。

3.1   含水层孔隙度对溶质运移的影响

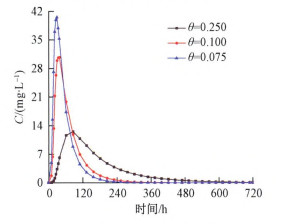
保持其它参数不变, 选取孔隙度分别为0.250、0.100, 0.075时, 对比不同孔隙度接收点浓度曲线变化(图 5)。从图 5可以看出, 当θ为0.25和0.1时, 浓度穿透曲线轻微不对称, 而θ当为0.075时, 浓度曲线显著不对称, 且拖尾较长。随着孔隙度的增大, 浓度曲线峰值依次为12.51, 30.68, 40.53 mg/L, 峰值到达时间依次为86, 38, 30 h, 曲线历时时间依次为710, 484, 388 h, 偏态系数分别为1.58, 1.25, 0.98。孔隙度越小, 浓度曲线峰值越大, 峰值到达时间越快, 曲线历时时间越短, 浓度穿透曲线越对称。

图  5  不同孔隙度接收点浓度曲线

Figure  5.  Concentration curves with different porosities

下载: 全尺寸图片 幻灯片

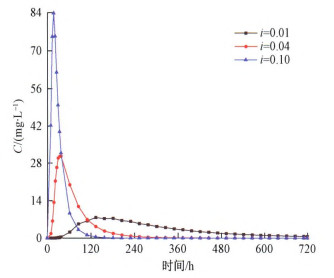
3.2   不同水力梯度对溶质运移的影响

保持其它参数不变, 选取水力梯度i分别为0.01, 0.04, 0.10时, 对比不同水力梯度接收点浓度曲线变化(图 6)。随着水力梯度增大, 浓度曲线峰值依次为4.55, 30.68, 82.52 mg/L, 峰值到达时间依次为134, 38, 18 h, 曲线历时时间依次为720, 484, 220 h, 偏态系数分别为0.74, 1.25, 0.52。水力梯度越大, 浓度曲线峰值越大, 峰值到达时间越快, 曲线历时时间越短。

图  6  不同水力梯度接收点浓度曲线

Figure  6.  Curves with different hydraulic gradients

下载: 全尺寸图片 幻灯片

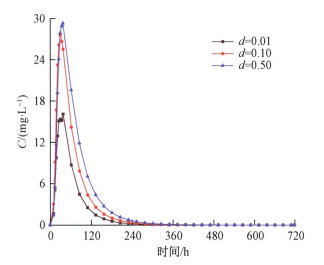
3.3   管道直径对溶质运移的影响

保持其它参数不变, 选取管道直径d分别为0.01, 0.10, 0.50时, 对比不同管道直径接收点浓度曲线变化(图 7)。随着管道直径增大, 浓度曲线峰值依次为16.09, 27.56, 29.32 mg/L, 峰值到达时间依次为38, 34, 38 h, 曲线历时时间依次为412, 460, 508 h, 偏态系数分别为1.02, 1.14, 1.30。管道直径越大, 浓度曲线峰值越大, 峰值到达时间基本相同。

图  7  不同管道直径接收点浓度曲线

Figure  7.  Curves with different conduit diameters

下载: 全尺寸图片 幻灯片

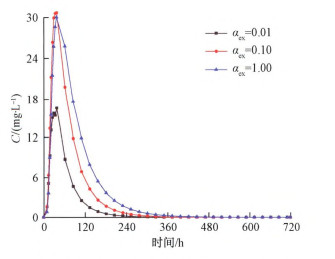
3.4   管道渗透系数α_ex对溶质运移的影响

保持其它参数不变, 选取管道渗透系数α_ex分别为0.01, 0.10, 1.00时, 对比不同管道渗透系数接收点浓度曲线变化(图 8)。随着管道渗透系数增大, 浓度曲线峰值依次为16.59, 30.68, 30.02 mg/L, 峰值到达时间依次为38, 38, 38 h, 曲线历时时间依次为412, 487, 604 h, 偏态系数分别为1.04, 1.25, 1.37。管道渗透系数越大, 浓度曲线峰值越大, 曲线越不对称, 峰值到达时间相同。

图  8  不同管道渗透系数接收点浓度曲线

Figure  8.  Curves with different pipe conductances

下载: 全尺寸图片 幻灯片

4.   结论

(1) 通过概念模型算例, 研究不同水文地质参数对溶质运移的影响, 发现随着水力梯度、管道直径及管道渗透系数的增大, 孔隙度减小, 浓度曲线峰值越大, 峰值到达时间越快, 浓度穿透曲线越对称, 为将来研究实际岩溶区溶质运移现象, 如示踪试验穿透曲线、尾矿库污染物在地下河出口的变化规律等提供科学基础。

(2) 管道流CFP模型能够刻画岩溶管道与基岩裂隙水流交换特征, 耦合MT3DMS溶质运移模型能够模拟穿透曲线的拖尾现象, 符合实际岩溶区特征, 为分析岩溶管道流溶质运移特征提供了一种有效手段。

(3) 实际岩溶区溶质运移浓度穿透曲线经常存在多峰曲线, 管道中存在溶潭、水流陡坎等不连续现象, 而CFP模型中仅用平直圆管概化岩溶管道特征, 与实际岩溶管道形态有一定出入; 精确刻画岩溶管道形态特征是进一步研究的目标。