运用地下水对潮汐的响应识别压力传导系数

阳玲; 杜金月; 王同科; 赵志学; 郝永红

doi:10.16030/j.cnki.issn.1000-3665.2019.06.04

运用地下水对潮汐的响应识别压力传导系数

阳玲^{1, 2,},
杜金月¹,
王同科¹,
赵志学¹,
郝永红^2, ,

1.
天津师范大学数学科学学院, 天津 300387
2.
天津师范大学天津市水资源与水环境重点实验室, 天津 300387

基金项目:

天津市自然科学基金重点项目 18JCZDJC39500

天津市高等学校创新团培养计划项目 TD13-5078

详细信息

作者简介:
阳玲(1993-), 女, 研究生, 主要从事数理统计研究。E-mail: 1334417805@qq.com

通讯作者:
郝永红(1964-), 男, 教授, 主要从事水文水资源方面的研究。E-mail: haoyh@sxu.edu.cn

中图分类号: P641.2
计量
- 文章访问数: 737
- HTML全文浏览量: 18
- PDF下载量: 505
出版历程
- 收稿日期: 2018-10-14
- 修回日期: 2018-12-13
- 刊出日期: 2019-10-31

Identification of hydraulic conductivity using the response of groundwater levels to oceanic tide

1.
College of Mathematical Science, Tianjin Normal University, Tianjin 300387, China
2.
Tianjin Key Laboratory of Water Resources and Environment, Tianjin Normal University, Tianjin 300387, China

HTML全文

摘要

摘要:
在地下水扩散方程中，压力传导系数是描述地下水运动的重要参数。传统的方法是通过抽水或注水给地下水系统一个扰动，监测地下水水位的响应，由此计算含水层的压力传导系数。文章提出用潮汐衰减率方法识别含水层压力传导系数，其适用于滨海区承压含水层的参数识别。在推导出解析解的基础上，通过数值拟合、最小二乘法、牛顿迭代法求得含水层的压力传导系数，提出潮汐衰减率的概念，建立余切函数与潮汐衰减率的线性关系，用线性关系中的斜率和截距识别压力传导系数。用潮汐衰减率方法识别出的压力传导系数与其实际值相等，说明该方法是正确有效的。潮汐信号衰减率与海水振荡的余切函数线性相关。数值仿真表明，该方法可以准确地估算出含水层的压力传导系数。潮汐衰减率方法具有少打井, 经济高效等优点。潮汐衰减率方法为实际工程应用提供了可靠的理论基础，它可以用于部分实际工程中。该方法的局限性在于需要提供含水层的部分参数，如含水层的长度、海水波动振幅、频率等。
- 地下水 /
- 潮汐 /
- 压力传导系数 /
- 牛顿迭代法 /
- 地下水扩散方程
Abstract:
Hydraulic conductivity is an important parameter describing groundwater movement in the groundwater diffusion equation. The traditional method is to give a disturbance to the groundwater system by pumping or injecting water, monitor the response of groundwater levels to the tide, and calculate the hydraulic conductivity of an aquifer. In this paper, a method of tidal attenuation rate is proposed to identify the hydraulic conductivity. It is suitable for identifying parameters of a confined aquifer in coastal areas. After deriving the analytical solution, the hydraulic conductivity of the aquifer is obtained by numerical fitting, least square method and Newton iteration method. The concept of tidal attenuation rate is proposed. The linear relationship between the cotangent function and the tidal attenuation rate is established. The slope and intercept of the linear relationship are used to identify the hydraulic conductivity. In this paper, the hydraulic conductivity identified by the method of tidal attenuation rate is equal to its actual value, showing that the method is correct and effective. The attenuation rate of tidal signals is linearly correlated with the cotangent function of sea water oscillation. The numerical simulation shows that the method can accurately estimate the hydraulic conductivity of the aquifer. The method of tidal attenuation rate has the advantages of less well-drilling, being economical and efficient. The tidal attenuation rate method provides a reliable theoretical basis for practical engineering applications and can be used in some practical projects. The limitation of this method lies in the need of some parameters of the aquifer, such as the length of the aquifer, the amplitude and frequency of sea water fluctuation, etc.
- groundwater /
- oceanic tide /
- hydraulic diffusivity /
- Newton iteration method /
- groundwater diffusion equation

HTML全文

世界上有40%的人口居住在离海岸线100 km以内的海滨城市, 给近海海域带来了大量污染, 破坏了生态环境^[1-3]。源于陆地的海洋污染有44%是来自于地下水海底排泄和地表径流^[1]。虽然地下水海底排泄的流量是地表河流入海径流量的40%^[2], 但是它的污染物浓度却是地表径流的10倍^[3]。海底地下水排放被视为海洋污染最主要的方式之一^[4-5]。预测海底地下水排放和输送到海洋中的污染物对海洋生态和环境保护有着重要意义。

水文地质参数识别又称水文地质逆问题求解, 是建立地下水数值模型的关键步骤^[6]。含水层的压力传导系数作为描述地下水溶质运移的关键参数被广泛的研究^[7-10]。传统识别压力传导系数最广泛的技术是抽水试验和振荡试验^[11-13], 但是这些方法有一个共同的缺点: 需要耗费大量的人力、财力和物力。为了更好地描述含水层的特性, 有必要开发一种经济高效的方法来估计含水层的压力传导系数。

海洋和河流的潮汐可以看作自然的振荡抽水试验, 可通过分析潮汐和地下水响应关系估计压力传导系数。Ferris估计了潮汐河含水层的压力传导系数, 他使用了时间滞后和潮汐与地下水位相关的潮汐效率因素的方法^[14]。Erskine估计了非承压和高度渗透沿海含水层的压力传导系数, 该含水层位于英国的一个核电站附近, 他用了时间滞后和潮汐效率因素方法^[15]。Zhou利用观测井观测地下水水位振幅和潮汐确定了T/S(给水度与导水系数之比), 写出了T/S的表达式^[16]。在贝尔港沿海岩溶含水层的背景下, 类似的压力传导系数的估计表明, 水动力环境包括基质、裂隙和管道流动系统。

然而, 前人运用地下水水位对潮汐的响应识别含水层的参数多采用数值拟合的方法。在前人的研究基础上, 本文试图获得潮汐产生的压力波在含水层中传播的解析解, 通过数值拟合估计含水层的压力传导系数。其能够更加清楚地了解潮汐影响地下水的机理。

1. 地下水模型

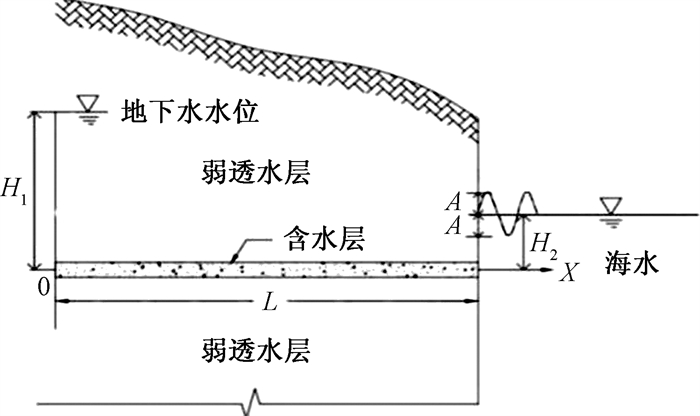
假设海滨区有一个水平、均质、等厚的含水层, 它位于两弱透水层之间(图 1)。因为地下水的压力水头高于含水层和海水的高度, 所以地下水向海中排泄。

图 1 滨海区含水层概念模型

l—含水层的长度；H₁—坐标原点处的地下水位；H₂—海水的平均水位；A—潮汐的振幅

Figure 1. Schematic diagram of the coastal aquifer

下载: 全尺寸图片幻灯片

基于图 1的概念模型, 建立笛卡尔直角坐标系, x轴的原点位于内陆, 距海岸的水平距离为l m, 且地下水水位是定水位H₁。x轴是水平的, 沿着含水层向海岸方向延伸, 垂直方向为海岸线方向。在实际条件中左边界为定水位边界的可能性不大, 更多的是流量边界。假设有一条与海岸平行的运河, 保证左边界为定水位边界。该模型需假设有一条与海岸平行的运河, 且该运河与海不相通。

承压含水层中地下水运动的一维偏微分方程为:

T \frac{\partial^{2} H}{\partial x^{2}} = S \frac{\partial H}{\partial t}, 0 < x < l

(1)

式中: H—水头/m;

x—水平坐标/m;

t—时间/h;

T—含水层的渗透系数/(m·h^-1);

S—含水层储水系数;

l—含水层的长度/m。

令 $D = \frac{T}{S} [L^{2} T^{- 1}]$ 式(1)变为:

D \frac{\partial^{2} H}{\partial x^{2}} = \frac{\partial H}{\partial t}, 0 < x < l

(2)

边界条件为:

{H |}_{x = 0} = H_{1}, {H |}_{x = l} = H_{2} + A \sin ω t, t > 0

(3)

式中: H₁—内陆含水层定水头边界/m;

H₂—海水平均水位/m;

A—海水振荡振幅/m;

ω—角速度/h^-1。

2. 地下水位对潮汐响应的解析解

将式(2)~(3)转化到复数域上^[17-18], 即将有关物理量从实平面扩充到复平面^[19]。变量x和t是相互独立的。因此可以用分离变量法求解:

H (x, t) = u_{1} (x, t) + u_{2} (x, t)

(4)

u_{1} (x, t) = H_{1} + \frac{H_{2} - H_{1}}{l} x

(5)

将式(4)代入式(1)~(3)中:

D \frac{\partial^{2} u_{2}}{\partial x^{2}} = \frac{\partial u_{2}}{\partial t}, 0 < x < l

(6)

u_{2} (0, t) = 0, u_{2} (l, t) = A \sin ω t t > 0

(7)

因为式(7)关于时间是周期的, 所以可以省略初始条件。把式(4)~ (6)扩张到复数域, 假设u₂(x, t)=lm(U(x, t)), 代入式(6)~(7), 可以得到:

D \frac{\partial^{2} U}{\partial x^{2}} = \frac{\partial U}{\partial t}, 0 < x < l

(8)

U (0, t) = 0, U (l, t) = A e^{i ω t}, t > 0

(9)

其中, $i = \sqrt{- 1}$ 用变量分离法解得:

\begin{aligned} U (x, t) = X (x) e^{i ω t} = & \frac{A e^{(1 + i) σ x + i ω t}}{e^{(1 + i) σ l} - e^{- (1 + i) σ l}} + \\ \frac{A e^{- (1 + i) σ x + i ω t}}{e^{- (1 + i) σ l} - e^{(1 + i) σ l}} \end{aligned}

(10)

\begin{matrix} H (x, t) = H_{1} + \frac{H_{2} - H_{1}}{l} x + \\ lm {\frac{A e^{(1 + i) σ x + i ω t}}{e^{(1 + i) σ l} - e^{- (1 + i) σ l}} + \frac{A e^{- (1 + i) σ x + i ω t}}{e^{- (1 + i) σ l} - e^{(1 + i) σ l}}} \end{matrix}

(11)

最终求解结果:

\begin{matrix} H (x, t) = H_{1} + \frac{H_{2} - H_{1}}{l} x + \\ A e^{\sqrt{\frac{ω}{2 D}} (l - x)} {[e^{2 / \sqrt{\frac{ω}{2 D^{x}}}} \cos (\sqrt{\frac{ω}{2 D}} (l + x) + ω t) - \\ \cos (\sqrt{\frac{ω}{2 D}} (l - x) + ω t)] [- e^{2 \sqrt{\frac{ω}{2 D} l}} \sin (2 \sqrt{\frac{ω}{2 D}} l)] + \\ [e^{2 / \sqrt{\frac{ω}{2 D} x}} \sin (\sqrt{\frac{ω}{2 D}} (l + x) + ω t) - \sin (\sqrt{\frac{ω}{2 D}} (l - x) + ω t)] \\ \frac{[- 1 + e^{2 \sqrt{\frac{ω}{2 D} l}} \cos (2 \sqrt{\frac{ω}{2 D}} l)]}}{[1 - 2 e^{2 \sqrt{\frac{ω}{2 D}} l} \cos (2 \sqrt{\frac{ω}{2 D}} l) + e^{4 \sqrt{\frac{ω}{2 D} l}}]} \end{matrix}

(12)

式(12)可以简化为:

H (x, t) = H_{1} + \frac{H_{2} - H_{1}}{l} x + α A \cos ω t + β A \sin ω t

(13)

其中:

\begin{aligned} α = & [- \sin h ((l + x) \sqrt{\frac{ω}{2 D}}) \sin ((l - x) \sqrt{\frac{ω}{2 D}}) + \\ \frac{\sin h ((l - x) \sqrt{\frac{ω}{2 D}}) \sin ((l + x) \sqrt{\frac{ω}{2 D}})]}{[\cos h (2 l \sqrt{\frac{ω}{2 D}}) - \cos (2 l \sqrt{\frac{ω}{2 D}})]} \end{aligned}

(14)

\begin{matrix} β = [\cos h ((l + x) \sqrt{\frac{ω}{2 D}}) \cos ((l - x) \sqrt{\frac{ω}{2 D}}) \\ \frac{- \cos h ((l - x) \sqrt{\frac{ω}{2 D}}) \cos ((l + x) \sqrt{\frac{ω}{2 D}})]}{[\cos h (2 l \sqrt{\frac{ω}{2 D}}) - \cos (2 l \sqrt{\frac{ω}{2 D}})]} \end{matrix}

(15)

3. 识别含水层的压力传导系数

由式(13)可知, 地下水水位由两部分组成: 第一部分是线性项 $H_{1} + \frac{H_{2} - H_{1}}{l} x$ , 这部分不依赖于时间, 表示没有潮汐波动时方程的解; 第二部分是波动项αAcosωt+βAsinωt, 表示地下水水位对潮汐的响应。线性部分是已知的, 所以只需研究地下水水位对潮汐的响应项:

\bar{H} (x, t) = α A \cos ω t + β A \sin ω t

(16)

r (x, t, ω) = \frac{\bar{H} (x, t)}{A \sin ω t} = α \cot ω t + β

(17)

式(17)表明潮汐信号衰减率r(x, t, ω)与余切函数cotωt线性相关。由实际观测到的潮汐数据和地下水响应数据, 可以根据式(17), 利用线性回归估计斜率α和截距β, 估计值分别用 $\hat{α}$ 和 $\hat{β}$ 表示。由式(14)、(15)可知斜率α与截距β都仅依赖于压力传导系数D, 因此可以根据估计值 $\hat{α}$ 和 $\hat{β}$ 数值求解式(14)或(15), 识别压力传导系数D。采用牛顿迭代法求解式(14)和(15), 迭代初值可以通过绘制α(D)和β(D)的函数图像获得。这种通过地下水水位对潮汐响应求含水层扩散系数的方法称为潮汐信号衰减率法。

4. 数值仿真

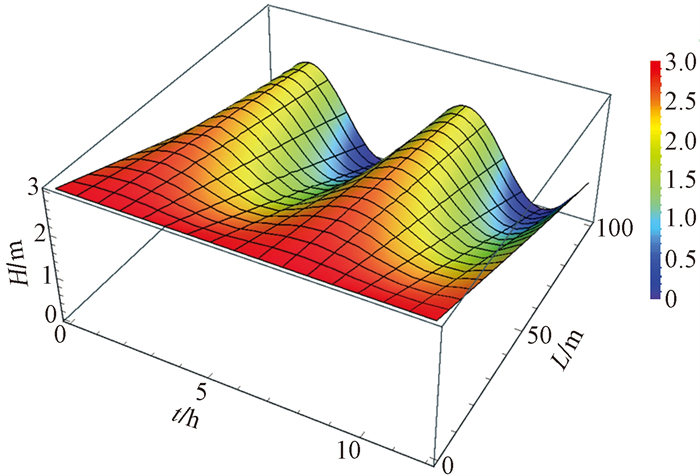
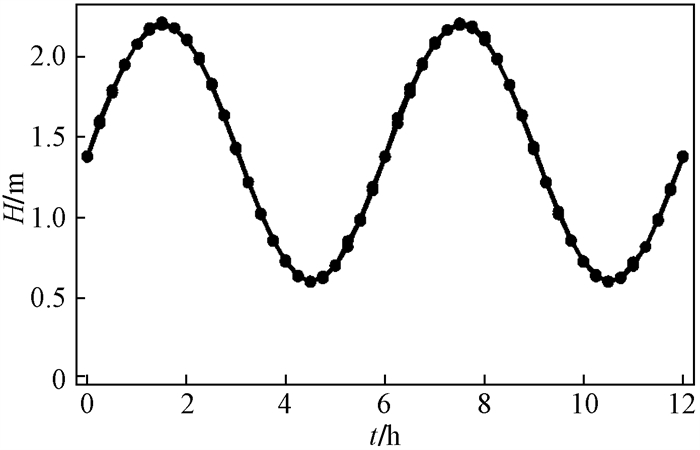
为了验证潮汐信号衰减率方法的正确性, 了解该方法的精度, 对式(13)中的参数赋值(表 1), 进行了数值仿真。赋值后由式(13)获得的地下水水位对潮汐的响应图, 见图 2。

表 1 含水层参数

Table 1. The parameter of aquifer

下载: 导出CSV

| 显示表格

图 2 地下水对潮汐的响应

Figure 2. Response of groundwater levels to oceanic tide

下载: 全尺寸图片幻灯片

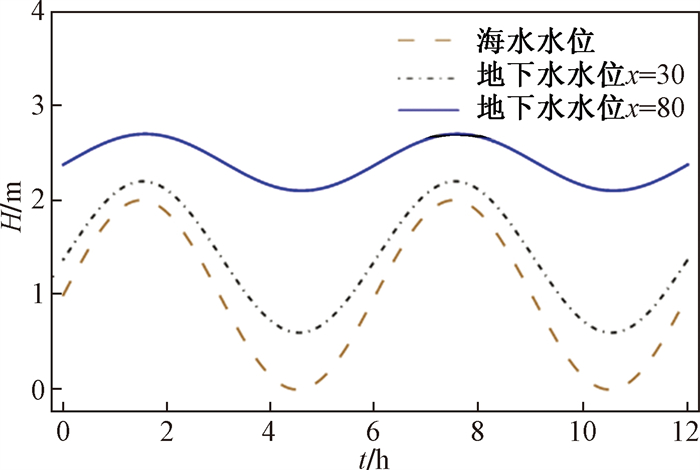
为更加清晰地了解不同位置地下水响应情况, 图 3表达了x=30 m和x=80 m以及海水水位三种不同情况下地下水水位随时间的变化。

图 3 x=30 m和x=80 m以及海水水位三种不同情况下地下水位随时间的变化

Figure 3. Change in groundwater levels with time at x=0 m, 30 m, 80 m

下载: 全尺寸图片幻灯片

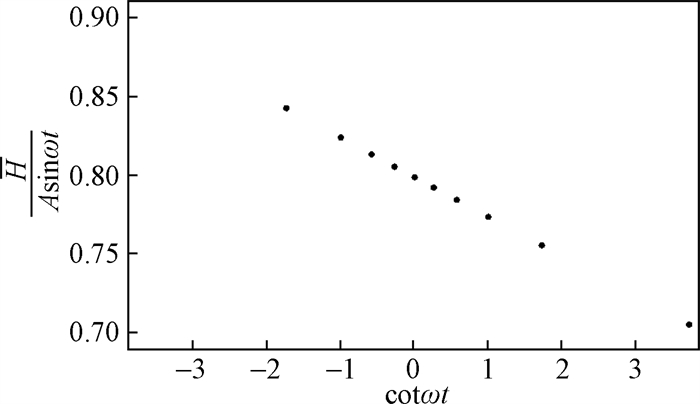
为检验潮汐衰减率r(x, t, ω)与余切函数cotωt之间的线性关系。当x=80 m时地下水水位, r(x, t, ω)与cotωt呈线性相关(图 4)。

图 4 x=80 m时r(x, t, ω)与cotωt的线性关系

Figure 4. Linear relationship betweenr(x, t, ω)and cotωt(b)when x=80 m

下载: 全尺寸图片幻灯片

为了验证潮汐信号衰减率方法的正确性, 模拟野外地下水水位的观测过程, 对x=80 m处的地下水数据进行取样, 取样时间步长为15 min, 共获得48个采样点(图 5)。

图 5 在x=80 m处，时间间隔为0.25 h, 地下水对潮汐响应的合成数据

Figure 5. Synthetic data of groundwater response to the oceanic tide at location of x=80 m and time interval of 0.25 h

下载: 全尺寸图片幻灯片

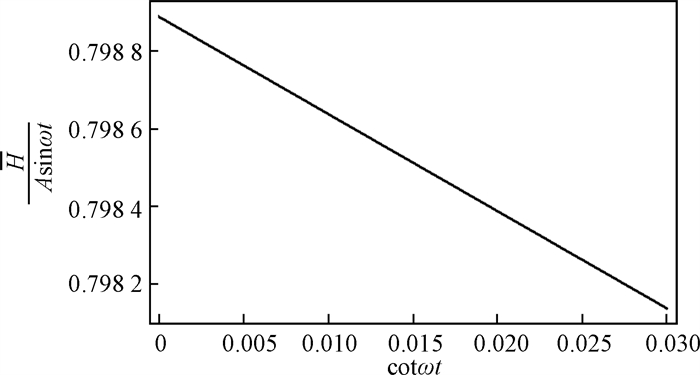
由图 6可见, r(80, t, ω)与cotωt呈线性关系。由于采样步长15 min, 相对于样本总体时间较小, 图 6中部分点重合。

图 6 潮汐信号衰减率r(x, t, ω)与cotωt的线性关系

Figure 6. Linear relationship between tide signal attenuation rate r(x, t, ω)and cot ωt

下载: 全尺寸图片幻灯片

对图 6数据进行最小二乘拟合, 可得斜率 $\hat{α} = - 0.0215$ 截距 $\hat{β} = 0.7989$ 。图 7能获得压力传动系数估计值 $\hat{D}$ 。为提高估计的精度, 可使用牛顿迭代法, 通常用目测估计得到的 $\hat{D}$ 作为牛顿迭代的初值^[20]。最后通过牛顿迭代法求得 $D = 20000 \frac{m^{2}}{h}$ 与表 1中给定的D完全吻合。通过数值仿真验证了潮汐衰减率方法正确性。

图 7 用α和β估计初值

\hat{D}

Figure 7. Estimation of the initial value

\hat{D}

with α and β

下载: 全尺寸图片幻灯片

5. 结论

(1) 在滨海含水层中, 地下水水位与海洋潮汐的交互作用类似于自然的振荡抽水试验。当涨潮时, 相当于给地下水注水, 地下水水位上升。当退潮时, 相当于抽取地下水, 地下水水位下降。基于潮汐信号在含水层中传播和衰减的过程, 建立地下水模型求得解析解, 提出用潮汐信号衰减率方法估计含水层的特性。潮汐信号衰减率r(x, t, ω)与海水振荡的余切函数cotωt线性相关。

(2) 线性关系中的斜率和截距都是压力传导系数的函数。提出了利用潮汐信号衰减率与余切函数的关系估计压力传导系数的方法(即用斜率和截距估计压力传导系数)。数值仿真结果表明, 该方法可以准确地估算含水层的压力传导系数D。

(3) 潮汐衰减率方法具有少打井, 经济高效等优点, 但也存在一定的局限性。在一般情况下含水层长度l值的获取需要一定的工作量, 在实际应用中需要根据情况权衡。

图 1 滨海区含水层概念模型

l—含水层的长度；H₁—坐标原点处的地下水位；H₂—海水的平均水位；A—潮汐的振幅

Figure 1. Schematic diagram of the coastal aquifer

下载: 全尺寸图片幻灯片

图 2 地下水对潮汐的响应

Figure 2. Response of groundwater levels to oceanic tide

下载: 全尺寸图片幻灯片

图 3 x=30 m和x=80 m以及海水水位三种不同情况下地下水位随时间的变化

Figure 3. Change in groundwater levels with time at x=0 m, 30 m, 80 m

下载: 全尺寸图片幻灯片

图 4 x=80 m时r(x, t, ω)与cotωt的线性关系

Figure 4. Linear relationship betweenr(x, t, ω)and cotωt(b)when x=80 m

下载: 全尺寸图片幻灯片

图 5 在x=80 m处，时间间隔为0.25 h, 地下水对潮汐响应的合成数据

Figure 5. Synthetic data of groundwater response to the oceanic tide at location of x=80 m and time interval of 0.25 h

下载: 全尺寸图片幻灯片

图 6 潮汐信号衰减率r(x, t, ω)与cotωt的线性关系

Figure 6. Linear relationship between tide signal attenuation rate r(x, t, ω)and cot ωt

下载: 全尺寸图片幻灯片

图 7 用α和β估计初值 $\hat{D}$

Figure 7. Estimation of the initial value $\hat{D}$ with α and β

下载: 全尺寸图片幻灯片

表 1 含水层参数

Table 1 The parameter of aquifer

下载: 导出CSV

参考文献(20)

[1]	International Maritime Organization(IMO). Inter-national shipping facts and figures-Information resources on trade, safety, security, environment[M/OL]. http://www.imo.org/en/KnowledgeCentre/ShipsAndShippingFactsAndFigures/TheRoleandImportanceofInternationalShipping/Documents/International%20Shipping%20-%20Facts%20and%20Figures.pdf#search=Share%20of%20the%20different%20sources%20of%20pollution%20into%20the%20marine%20environment.
[2]	MOORE WS, AMOLD R. Measurement of ²²³Ra and ²²⁴Ra in coastal waters using a delayed coincidence counter[J]. Journal of Geophysical Research, 1996, 101(Sup1): 1321-1329.
[3]	LAMONTAGNE M G, DURAN R, VALIELA. Nitrous oxide sources and sinks in coastal aquifers and coupled estuarine receiving waters[J]. Science of the Total Environment, 2003, 309(1/2/3): 139-149.
[4]	SHEN P X, WANG S J, CLARE R. Memory of past random wave conditions in submarine groundwater discharge[J]. Geophysical Research Letters, 2014, 41(7): 2401-2410. DOI: 10.1002/2014GL059617
[5]	MOORE W S. The effect of submarine groundwater discharge on the ocean[J]. Annual Review of Marine Science, 2010(2): 59-88.
[6]	骆乾坤, 王佩, 朱国荣. 水文地质参数识别的快速和谐搜索算法[J]. 水文地质工程地质, 2011, 38(4): 14-19. https://www.swdzgcdz.com/article/id/201104003 LUO Q K, WANG P, ZHU G R. Fast harmony search algorithm and its application to hydrogeological parameters identification[J]. Hydrogeology & Engineering Geology, 2011, 38(4): 14-19. (in Chinese) https://www.swdzgcdz.com/article/id/201104003
[7]	GUO H P, JIAO J J, LI H L. Groundwater response to tidal fluctuation in a two-zone aquifer[J]. Journal of Hydrology, 2010, 381(3/4): 364-371.
[8]	PACHECO FAL, LANDIM P M B, SZOCS T. Bridging hydraulic diffusivity from aquifer to particle-size scale: a study on loess sediments from southwest Hungary[J]. Hydrological Sciences Journal-journal Des Sciences Hydrologiques, 2015, 60(2): 269-284.
[9]	TREFRY M G, JOHNSTON C D. Pumping test analysis for a tidally forced aquifer[J]. Ground Water, 1998, 36(3): 427-433. DOI: 10.1111/j.1745-6584.1998.tb02813.x
[10]	DOAN M L, BRODSKY E E, KANO Y, et al. In situ measurement of the hydraulic diffusivity of the active Chelungpu Fault, Taiwan[J]. Geophysical Research Letters, 2006, 33(16): L16317.
[11]	LI V C. Estimation of in-situ hydraulic diffusivity of rock masses[J]. Pure and Applied Geophysics, 1984, 122(2/4): 545-599.
[12]	KAMP GVD. Methods for determining the in situ hydraulic conductivity of shallow aquitards-an overview[J]. Hydrogeology Journal, 2001, 9(1): 5-16. DOI: 10.1007/s100400000118
[13]	RASMUSSEN T C, HABORAK K G, YOUNG M H. Estimating aquifer hydraulic properties using sinusoidal pumping at the Savannah River site, South Carolina, USA[J]. Hydrogeology Journal, 2003, 11(4): 466-482.
[14]	FERRIS J G. Cyclic fluctuations of water level as a basis for determining aquifer transmissibility[J]. Int Assoc Hydrolog Sci, 1951, 33(2): 148-155. https://pubs.usgs.gov/publication/70133368
[15]	ERSKINE A D. The effect of tidal fluctuation on a coastal aquifer in the U K[J]. Ground Water, 1991, 29(4): 556-562.
[16]	ZHOU X, SONG C, LI T. Estimation of aquifer parameters using tide-induced groundwater level measurements in a coastal confined aquifer[J]. Environmental Earth Sciences, 2015, 73(5): 2197-2204. DOI: 10.1007/s12665-014-3570-5
[17]	LI H L, JIAO J J. Analytical studies of groundwater-head fluctuation in a coastal confined aquifer overlain by a semi-permeable layer with storage[J]. Advances in Water Resources, 2001, 24(5): 565-573.
[18]	TOWNLEY L R. The response of aquifers to periodic forcing[J]. Advances in Water Resources, 1995, 18(3): 125-125.
[19]	李海龙, 宋金颖, 万力, 等. 承压含水层井孔储存效应对气压波动引起的井孔水位波动的影响[J]. 水文地质工程地质, 2013, , 40(4): 1-6. https://www.swdzgcdz.com/article/id/20130401 LI H L, SONG J Y, WAN L, et al. The response of well-aquifer systems to barometric loading[J]. Hydrogeology & Engineering Geology, 2013, 40(4): 1-6. (in Chinese) https://www.swdzgcdz.com/article/id/20130401
[20]	DEUFLHARD, PETER, HOHMANN, ANDREAS. Numerical analysis in modern scientific computing. An Introduction[M]. 2nd ed. New York: Springer Press, 2003: 81-117.

施引文献(1)

期刊类型引用(1)

黄长生，侯保全，易秤云，李龙，张胜男，周耘，Waseem Akram，王芳婷. 赣南地热水形成条件分析与赣县区地热水勘查靶区圈定. 华南地质. 2021(01): 64-74 .

百度学术

其他类型引用(0)

资源附件(0)

图(7) / 表(1)

计量

文章访问数: 737
HTML全文浏览量: 18
PDF下载量: 505
被引次数: 1

1. 地下水模型
2. 地下水位对潮汐响应的解析解
3. 识别含水层的压力传导系数
4. 数值仿真
5. 结论

运用地下水对潮汐的响应识别压力传导系数

作者简介:
阳玲(1993-), 女, 研究生, 主要从事数理统计研究。E-mail: 1334417805@qq.com

通讯作者:
郝永红(1964-), 男, 教授, 主要从事水文水资源方面的研究。E-mail: haoyh@sxu.edu.cn

计量