岩土的渗透性，是指岩土透过水或其他流体的性能^{[1 − 4]}。渗透系数也称水力传导率，是表征水在岩土中渗透性的指标^{[5 − 7]}，是确定水库渗透量、进行地下水资源计算、开展溶质运移规律研究等不可或缺的重要的水文地质参数^[8]，是解决绝大多数地下水流动问题的前提条件^{[9 − 10]}。1856年法国工程师达西通过试验得出达西定律（Darcy’s law）^{[11 − 14]}，其表达式为：

式中：Q——渗透流量/（cm³·s⁻¹）；

K——渗透系数/（cm·s⁻¹）；

A——过水断面的面积/cm²；

H₁、H₂——上下游过水断面的水头/cm；

L——上下游过水断面的距离/cm；

J——水力坡度。

自然环境中渗透介质和流体千变万化，达西试验的结果与实际情况通常存在差异^{[15 − 16]}。前人已对达西试验结果影响因素做过部分研究工作。经验表明，水的状态影响着渗透系数。姜伟男等^[17]以典型砂介质为研究对象，配制不同盐度的NaCl溶液，采用室内常水头试验，定量分析盐度变化对渗透介质渗透系数的影响。众多学者^{[18 − 22]}系统研究了水力梯度对渗透系数的影响，研究表明渗透系数与水力梯度呈负相关关系。陈四利等^[23]发现水泥土和软岩的渗透系数均随着温度增加而逐步增大；水泥土在海水环境下的渗透系数大于同温度的清水环境。

砂介质状态亦对渗透系数的变化有至关重要的作用。李龙飞^[24]对不同粒径砂样及2种不同粒径按照不同的质量比混合后的砂样进行渗流试验，研究岩土颗粒粒径大小及其质量比对渗透性的影响，确定了基于渗透性的岩土粒径临界值。韩立炜等^[25]和Radford等^[26]通过试验证明了压实后渗透介质密度明显增大，渗透系数显著降低。李华等^[27]和张镇飞等^[28]对不同干密度压实黄土进行试验研究，发现渗透性曲线与基质吸力的关系，证明了渗透系数与孔隙分布密切相关，孔隙越多渗透性越强。与此同时，丁瑜等^[29]对93组粗粒土全级配研究发现孔隙比与渗透系数呈正相关关系，且对渗透系数的影响大于其他粒径特征；相同级配的粗粒土随孔隙比变化可使渗透系数产生数量级跨越。

为了系统讨论多个因素的影响效果并进行对比研究，作者基于传统达西试验原理^[30]，改进达西试验装置，通过调节供水室高度改变供排水头差，选择3种砂介质即细砂、中砂、粗砂，分别开展改变水温、溶解性总固体（total dissolved solids，TDS）、供排水头差和压实程度的试验，并对结果进行对比分析，验证中细砂的雷诺上限问题，将对今后渗透系数的获取、应用提供借鉴，为地下水评价、地质灾害防治等水文地质工作中参数选取提供依据。

1.   试验装置与材料方法

1.1   达西试验仪

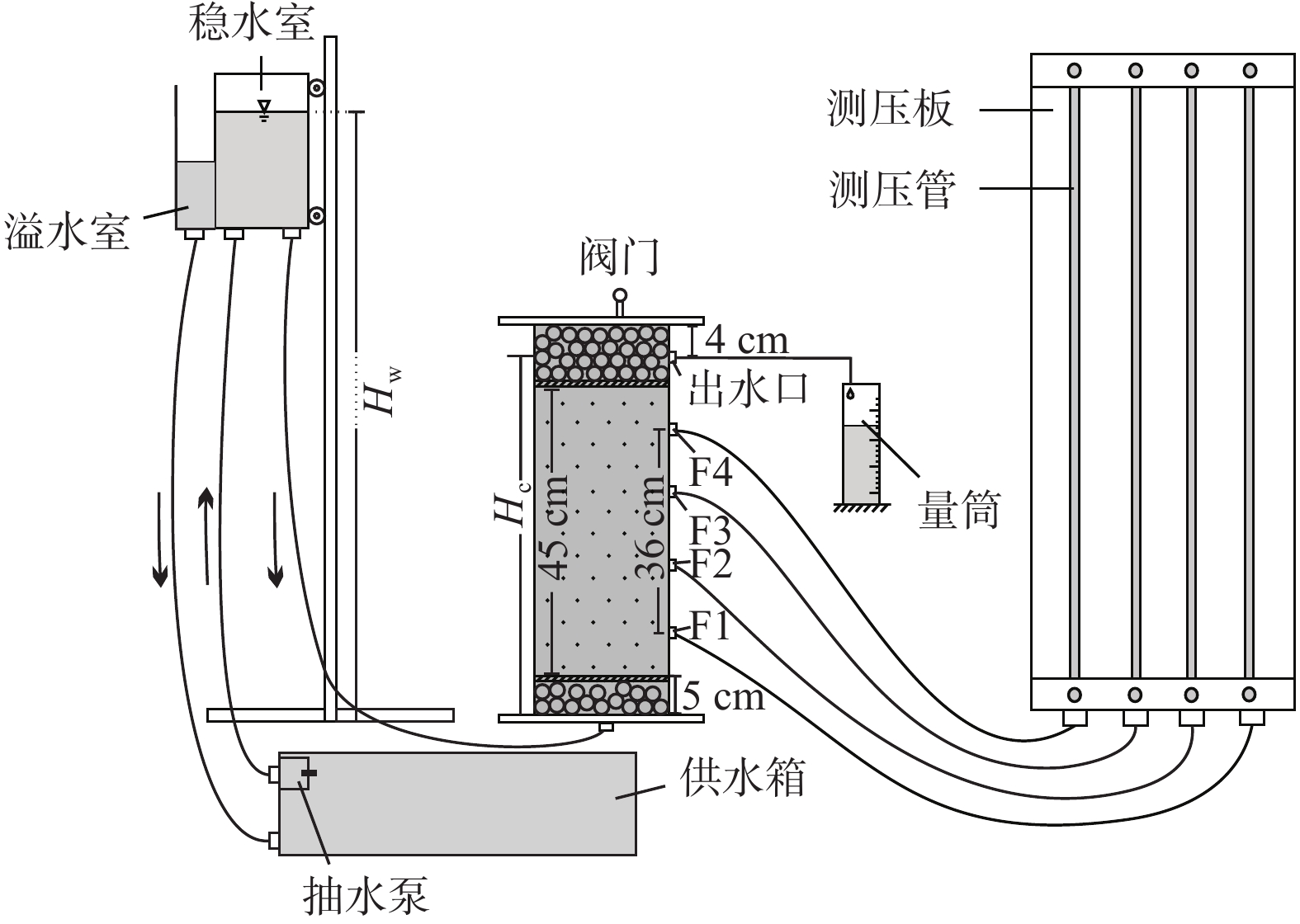
与传统的达西试验仪相同，试验装置包含供水、渗透、测压、排水4部分（图1），所不同的是采用了可变水头的供水装置，可较大程度地提高供排水的水头差。

图  1  达西试验装置

Figure  1.  Darcy test device

下载: 全尺寸图片 幻灯片

（1）供水部分

由可垂向升降的稳水室、溢水室和含抽水泵的供水箱组成。稳水室底部与渗透圆筒底部进水口相连，稳水室水面到渗透圆筒底部距离为稳水室水位高度（H_w）。当水泵入稳水室后，部分水进入渗透圆筒，多余的部分进入溢水室，再流入供水箱，形成循环，以确保稳水室的水头稳定，即保持每次试验供水的水头不变。每次试验，均测量稳水室的高度。

（2）渗透部分

采用有机玻璃砂柱圆筒装满砂介质，本次试验采用3种不同粒径的砂。圆筒内直径15 cm，上部设有排气阀门，底部设有进水口。圆筒壁侧设有出水口和间距均为12 cm的4个测压孔F1、F2、F3、F4，每个测压孔用胶管连接测压板上相应的测压管。

（3）测压部分

在测压板上设置4条玻璃测压管，每条测压管旁设有标尺，下端口分别用胶管与砂柱圆筒上对应的测压孔F1、F2、F3、F4连接。

（4）排水部分

包括砂柱圆筒右侧的出水口及量筒。出水口至渗透装置底部进水口之间距离为53 cm，称为出水口中心的水位高度（H_c），故H_c=53 cm。

出水口设有旋钮，借此可以控制出水量。测量某时间段内出水口的流量即为观测流量（Q_c），出水口流量除以时间即为单位时间流量，简称渗流量（Q）。渗流量除以圆筒横截面积，即可得出渗透流速（v）。

稳水室水位与砂柱圆筒出水口的中心水位之间的水头差，称为供排水间的总水头差（H），即H=H_w−H_c。通过上下移动稳水室高度，可调节供排水间的总水头差。

1.2   试验用砂属性

石英砂物理化学性质稳定，渗透性良好，故本次试验将细、中、粗3种粒径的石英砂作为试验材料，用圆孔标准筛进行筛分，分别得到0.10～0.25 mm、0.25～0.50 mm、0.50～2.00 mm共3个粒径（d）区间，得到试验所需的3种砂样，见表1。

表  1  试验用砂介质参数

Table  1.  Sand media parameters used for the test

砂介质类型	粒径/mm	一般捣实程度的质量/g
细砂	0.10≤d≤0.25	13414
中砂	0.25<d≤0.50	13543
粗砂	0.50<d≤2.00	13673

下载: 导出CSV 

| 显示表格

1.3   试验方法

为探究不同条件下达西试验产生的不同结果，在常温常压下的室内实验室中，对不同粒径的砂介质开展不同温度、TDS、供排水水头差等试验。

（1）先将砂样用稀盐酸浸泡，再用清水反复冲洗并烘干。装样前在砂柱顶、底部滤板上铺一层5 cm厚的粒径为2 cm的玻璃球，覆以纱网，防止砂样泄漏。将砂样称重后，按照每3～5 cm一层均匀铺入圆筒，直至装满渗透装置并用捣棒捣实。砂柱高度45 cm。

（2）确定稳水室高度，打开抽水泵，调节进水量，确保稳水室呈溢水状态；敞开圆筒顶部排气阀门，水流入圆筒进水口后，自下而上饱和砂样；确认圆筒气体排净、充满水后，关闭圆筒顶部排气阀门；打开测压管止水夹，去除胶管内的气泡；观察所有测压管水位，若在同一水平面上，即可开始试验。

（3）调节出水口阀门，控制不同的出水口水量，待稳定后，读出测压板的水头值。

（4）重复上述步骤，开展多次试验，测定出不同温度、TDS、水头差、捣实程度与砂样粒径的渗透流量及水头差。

为确保数据的可靠性，本次试验采取以下措施。每种试验分别进行3次，取平均值以减小误差；在每次进行不同TDS的试验前，先用待试验盐度的盐水反复冲洗砂柱，并测定排出水的TDS，当排出水的TDS与试验用盐水相同时，再进行试验。不同温度的情况不好处置，实验室环境温度在18～25 °C之间，砂柱圆筒不具有隔热功能，因而散热效应会使得其进水口温度与出水口温度存在温度差。温度高时，温差达到5～8 °C，这是本次试验不能排除的误差所在。为使进水口与出水口温度的温差最小，采取保持进水水温稳定的情况下，进行较长时间、最大流量排水，当出水口温度达到稳定后，读取流量及测压水位值，之后逐次减小流量再进行试验。为保证数据一致性，本次试验采用的温度值，均为出水口温度，特作说明。

2.   试验结果与分析

本试验采用细、中、粗3种砂介质，过水断面面积（A）为176.625 cm²。因试验过程中，4个测压孔的压力差一直保持线性关系。故如无特指上下游过水断面距离均为F4与F1的距离，即渗透途径（L）为36 cm，计算水力坡度采用的水头差（∆H）为F4与F1对应的测压管的水头差：

式中：v——渗流速度/（cm·s⁻¹）；

∆H——水头差/cm。

2.1   水温的影响

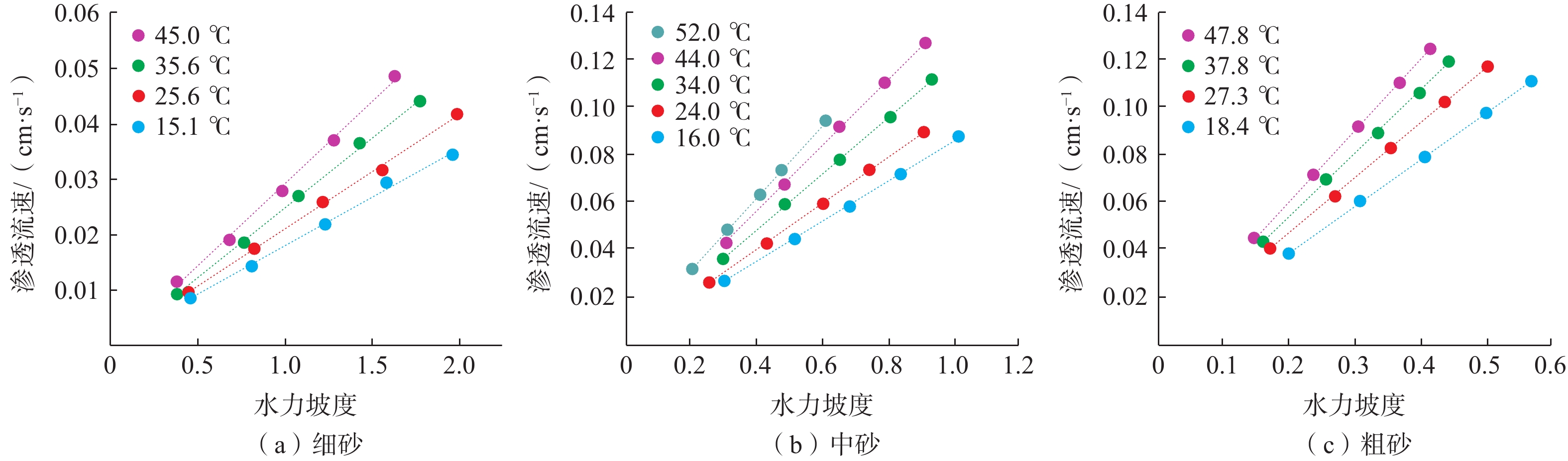
对于某一种砂介质，在某种试验温度时，读取最大出水量及其对应的各个测压管的水位，然后逐次减少出水量，见图2。

图  2  不同温度下水力坡度与渗透流速的线性关系

Figure  2.  Linear relationships between hydraulic gradient and seepage flow rate at different temperatures

下载: 全尺寸图片 幻灯片

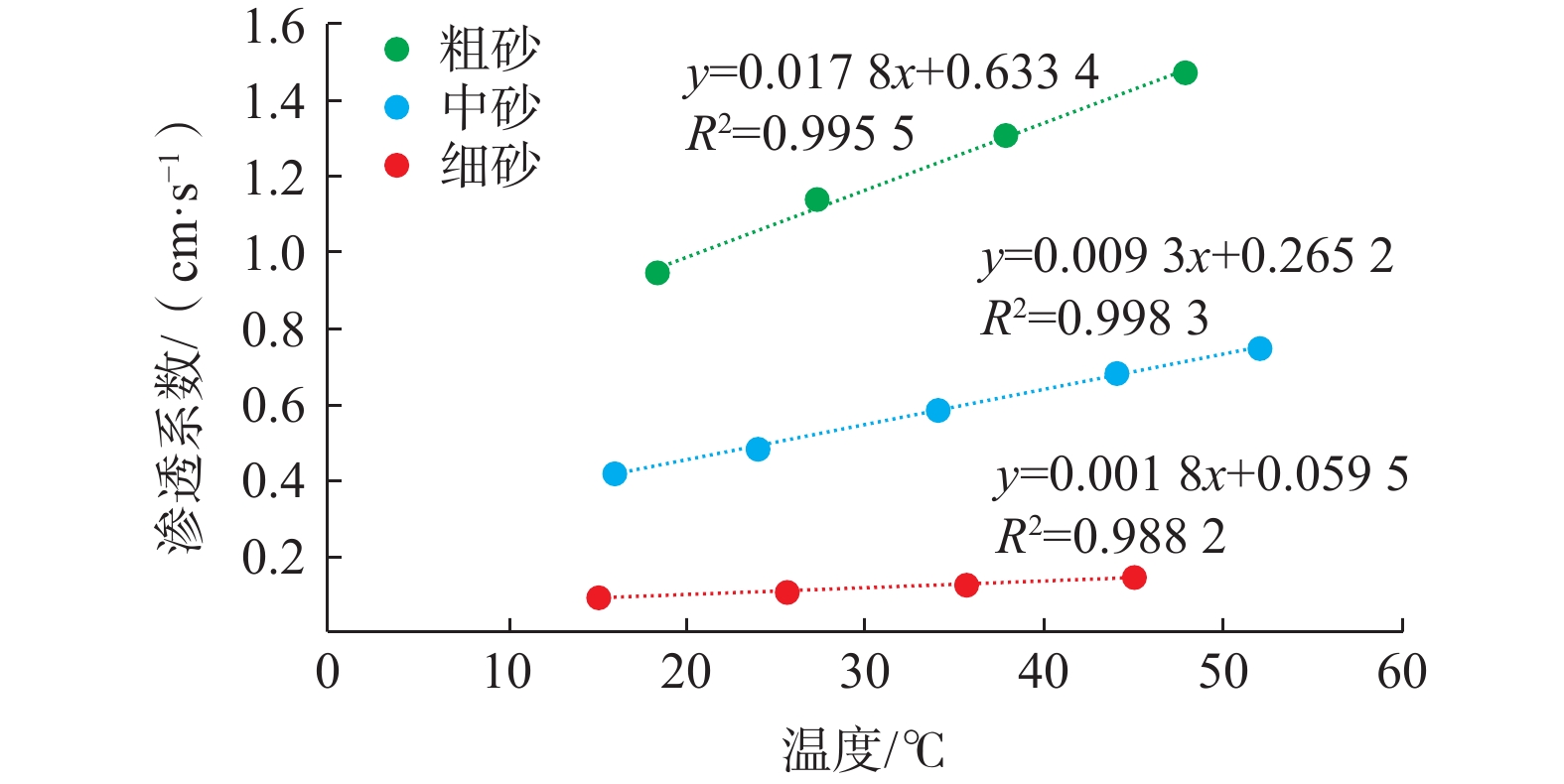
可以看出，同一温度条件下，细、中、粗砂介质渗透流速均随水力坡度增大而升高，且呈良好线性关系，R²>0.99。由此得出，水温升高，可增加砂介质渗透性。这与水的黏滞性随温度升高而降低所得出的结论是一致的。图2中水力坡度与渗透流速的线性关系的斜率是渗透系数，与温度的对应关系见图3。砂介质渗透系数亦随增温而升高，且温度变化时，不同砂介质的渗透系数均随之发生了变化，但变化程度不同。

图  3  不同砂介质温度与渗透系数的线性关系

Figure  3.  Linear relationships between temperature and hydraulic conductivity of different sand media

下载: 全尺寸图片 幻灯片

对3种砂介质情况进行对比发现，粗砂在温度升高时，渗透系数与温度的线性关系斜率最大，渗透系数变化最明显，即温度对其渗透性影响最大，温度从18 °C升高到48 °C增加了大约0.5 cm/s。细砂渗透系数随升温增加缓慢，从15 °C升高到45 °C仅增加大约0.05 cm/s。中砂介于两者之间。

由此得出，砂介质越粗，渗透流速变化速率越快，即粗砂时，温度的影响比细砂更强烈。换言之，渗透性好的介质比渗透性差的介质随温度变化的趋势更为显著，且温度在15～60 °C之间变化时，渗透系数与温度的变化是线性的。

2.2   TDS的影响

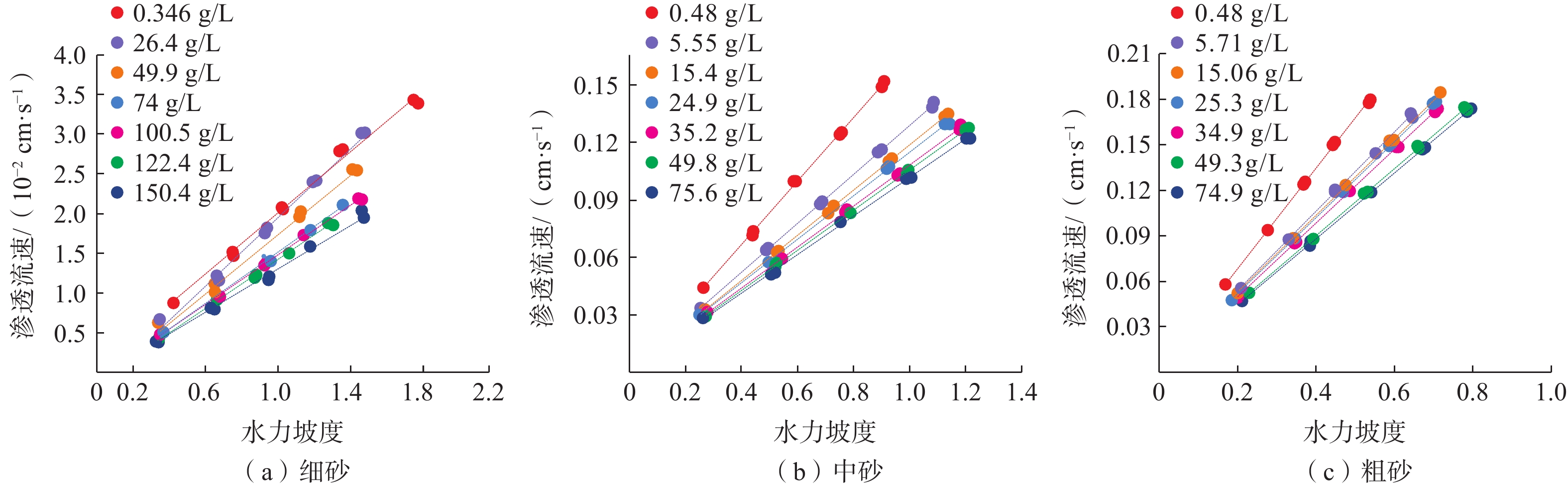
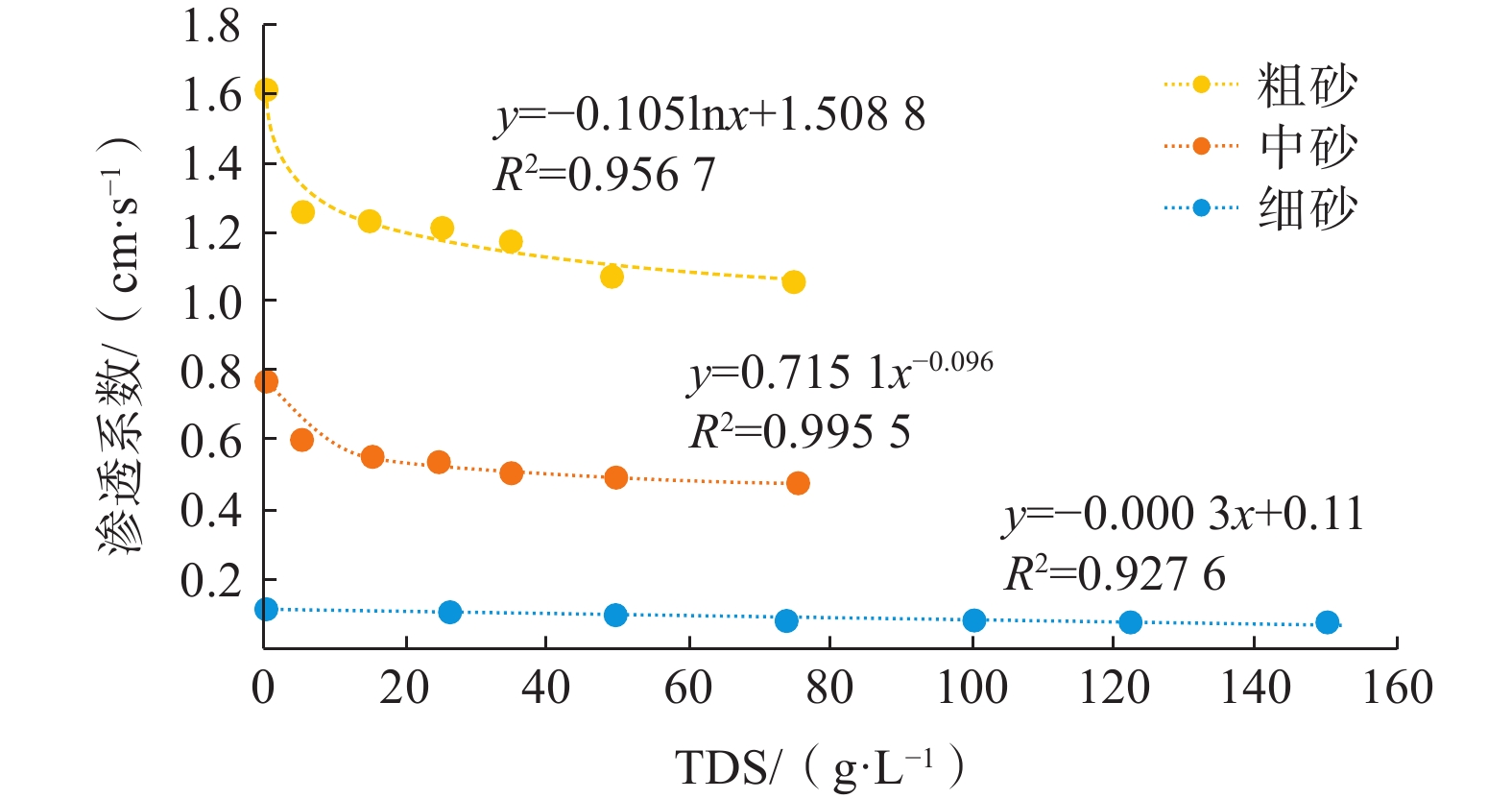
为了对比TDS对砂介质渗透性的影响，本试验在常温、标准大气压下由低到高改变TDS浓度，针对细、中、粗砂分别设置了7组不同TDS的水进行试验，见图4。

图  4  不同TDS水的水力坡度与渗透流速的线性关系

Figure  4.  Linear relationships between hydraulic gradient and seepage flow rate of water with different salinity

下载: 全尺寸图片 幻灯片

可以看出，水力坡度越大、砂介质越粗、TDS越小，渗透流量越大，水的渗透性越强，反之亦然。不论砂介质粗细，TDS变化对渗透流速的影响均是线性反比的，TDS越高，渗透流速越小。线性关系的斜率即为其渗透系数。TDS及其对应渗透系数的关系，见图5。

图  5  不同砂介质TDS与渗透系数的关系曲线

Figure  5.  Relationship curves between salinity and hydraulic conductivity in the different sand media

下载: 全尺寸图片 幻灯片

可以看出，每种砂的渗透系数也是随着水的TDS的变化而变化，但是其变化趋势与温度的影响有差别。粗砂和中砂在TDS较低时引起的渗透系数的变化要大于高TDS的情形。

当为细砂介质时，随TDS由低到高，渗透系数近似均匀减小，TDS从0.346 g/L升高至150.4 g/L，渗透系数从0.1114 cm/s降低至0.0719 cm/s。经回归分析，两者呈线性相关关系，y=−0.003x+0.11（y为渗透系数，x为水的TDS），R²=0.9276。

当为中砂介质时，随TDS的升高，渗透系数先快速下降，在TDS升高至30 g/L时，渗透系数下降速度开始减小，关系曲线趋于平缓。经回归分析，两者呈幂函数关系y=0.7151x^−0.096（y为渗透系数，x为水的TDS），R²>0.99，说明函数关系拟合得很好。

当为粗砂介质时，低TDS时，渗透系数随TDS的升高而下降的速度比中砂时更快，当TDS达到60 g/L时，渗透系数变化才趋于平稳，由试验数据回归分析生成的关系函数更倾向于对数函数y=−0.105lnx+1.5088（y为渗透系数，x为水的TDS），R²=0.9567。

综上，TDS增加砂介质渗透性减弱。对于不同砂介质，渗透系数变化趋势存在差异：粗砂介质渗透性最好，TDS变化引起的渗透性改变是非线性的，近似于对数函数，低TDS时更敏感，高TDS时趋平缓；细砂介质渗透性最差，TDS变化对细砂介质渗透性的影响趋近于线性，渗透系数始终低于0.2 cm/s；中砂介质的变化情况介于两者之间。

2.3   供排水水头差的影响

由上可知，水温和TDS都对砂介质渗透性有影响，尽管存在多种差异，但水力坡度与渗透流速之间一直存在很好的线性关系，即符合达西定律。

受到条件限制，试验中温度（出水口温度）没有超过60 °C，TDS保持在150 g/L以下，对于更高温度和更高TDS的情况，本次没有设计相应的试验。与之不同的是，供排水水头差的变化对渗透性改变的试验，超出了达西定律所规定的线性范围。

前已述及，本次试验装置（图1）的砂柱圆筒的出水口位置高度固定不变，但作为供水的稳水室是可以上下移动的，即稳水室水位和供排水间总水头差是变化的。

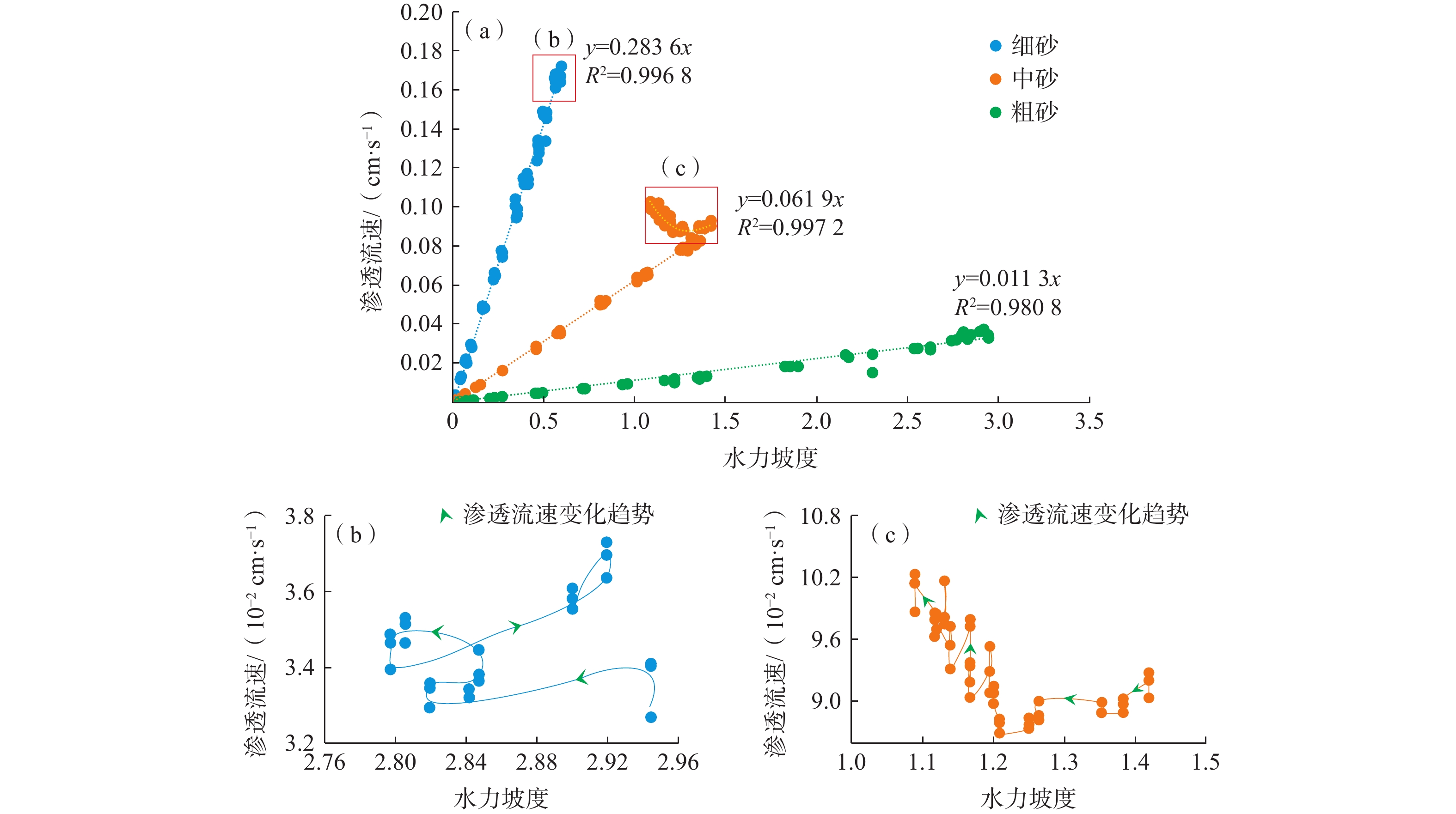
本次试验用水是低TDS的常温（室温）水，采用了与上述相同的细、中、粗3种砂。每次试验，均固定稳水室高度，然后通过改变出水口流量，并读取对应测压水管水位，计算水力坡度和渗透流速，两者关系见图6。

图  6  不同供排水水头差条件下水力坡度与渗透流速的关系

Figure  6.  Relationships between hydraulic gradient and seepage flow rate under different water supply and drainage head differences

下载: 全尺寸图片 幻灯片

每种砂的渗透流速亦随水力坡度的增大而增大，其中细砂变化最快，中砂变化幅度居中，粗砂最慢，变化速度比大致为28∶6∶1，在未超出达西定律规定范围内呈现良好线性关系。但在细砂和中砂的关系曲线的右上端，均出现了不规则的混乱点，其渗透流速不再随着水力坡度的增大而线性增大，图6（b）与图6（c）分别为细、中砂渗透流速变化异常的局部放大图。在供排水水头差的变化对渗透性影响试验中，对于变化敏感的细、中砂，水头差增大到一定程度，超出了达西定律所规定的线性范围，此时再增大供排水水头差，渗透流速不再发生规律性变化，渗透系数也不再是一个常数。

2.4   压实度的影响

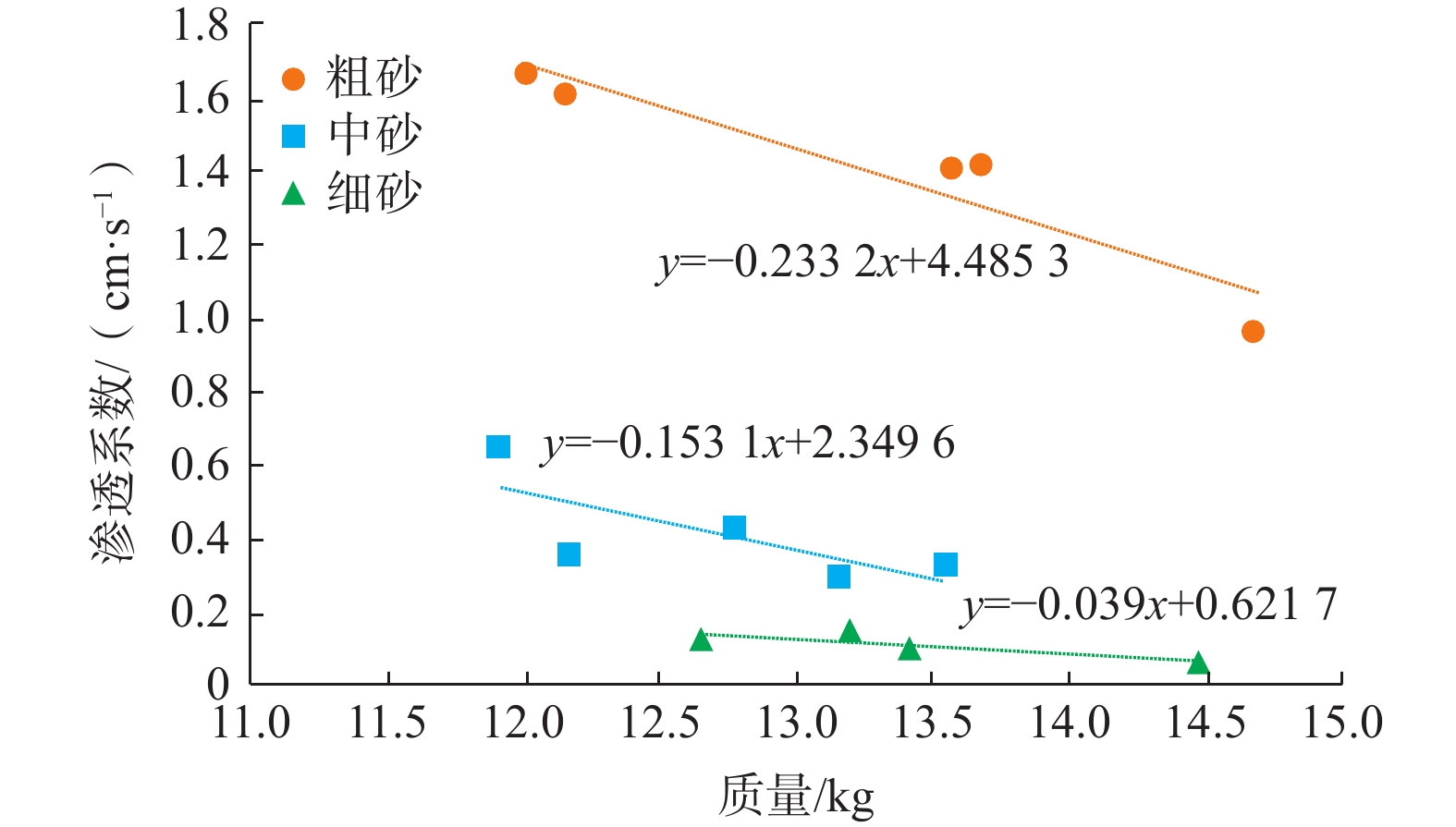
砂柱圆筒体积是不变的，但是人工捣实程度加重，可增加砂粒压实度。本次利用充满砂柱圆筒所需要的砂粒的质量表征压实度，显然用砂量越多，其压实度越大。细、中、粗3种砂质量变化与渗透系数的关系曲线，见图7。

图  7  不同砂介质压实度与渗透系数的线性关系

Figure  7.  Linear relationships between the degree of compaction and the hydraulic conductivity of different sand media

下载: 全尺寸图片 幻灯片

砂粒质量越大，压实度越高，其渗透系数越小，两者呈显著的负增长关系；砂介质越粗，线性关系中斜率的绝对值越大，反之亦然；所用砂质量相同时，砂介质越粗，介质的渗透系数越大，说明压实度相同时，粗砂的有效孔隙度比细砂大，见图8。

图  8  水流在压实后的砂介质中的运动状态模型

Figure  8.  Model of motion state of water flow in a compacted sand medium

下载: 全尺寸图片 幻灯片

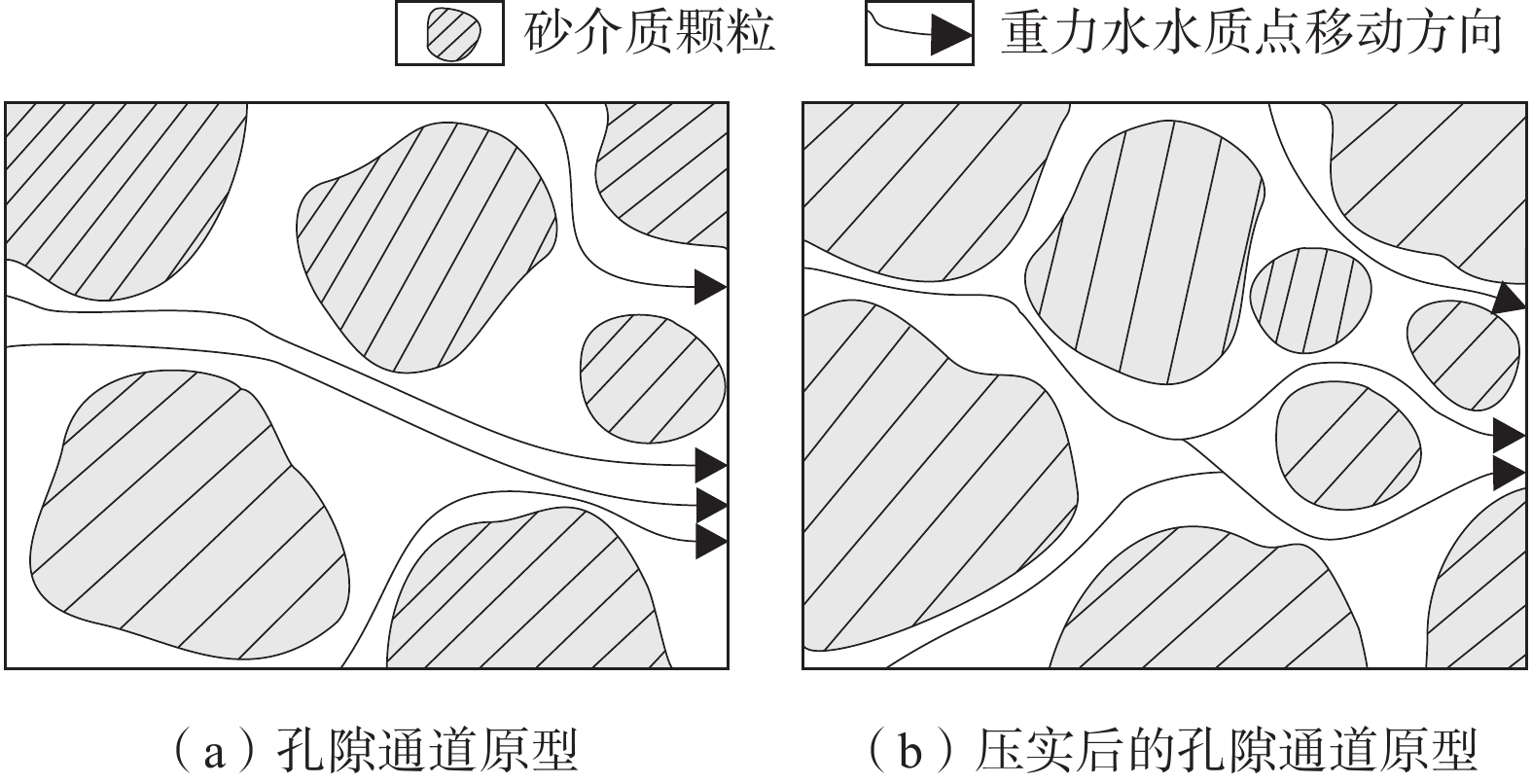
从微观角度分析，压实度越高，颗粒排列越紧密，孔隙及孔隙度均越小。而孔隙大小，对于砂介质滞留、释出及传输水的能力影响很大。如图8所示，孔隙边缘分布结合水层，中间为重力水。结合水一般不流动；临近结合水层的重力水，因隙壁吸引流动缓慢；越远离介质颗粒，水质点运动速度越快。对砂介质进行压实操作后，孔隙直径变小，水质点平均流速变小，渗透性变差。可以预见，当孔隙直径等于或小于结合水厚度两倍时，介质导水性能将几乎丧失，砂介质甚至出现良好的隔水性能。

2.5   砂介质粒径大小的影响

根据上述对温度、水头差、TDS和砂介质压实度对渗透系数的影响分析可以看出，砂介质粒径是影响渗透性的主要因素之一，砂介质粒径越大，砂介质越粗，试验变量变化越明显。

试验所用细、中、粗3种砂样，通过圆孔标准筛，得到砂样粒径区间分别为0.10～0.25 mm、0.25～0.50 mm、0.50～2.00 mm，试验用砂量由于捣实程度不同而不同。砂样圆筒总体积为7948.125 cm³，由填充砂的质量可求出其干密度（ρ_d），利用由比重瓶法测定的各粒径区间砂土颗粒的相对密度（ρ_s），即可计算出孔隙度（n），见表2：

表  2  各粒径级砂介质的相关参数

Table  2.  Relevant parameters of graded sand media of each particle size

砂介质 类型	粒径/mm	质量/g	干密度 /（g·cm−3）	相对密度 /（g·cm−3）	孔隙度/%
细砂	0.10≤d≤0.25	12634	1.590	2.665	40.35
		13192	1.660		37.72
		13414	1.688		36.67
		14475	1.821		31.66
中砂	0.25<d≤0.50	11914	1.499	2.657	43.58
		12171	1.531		42.37
		12771	1.607		39.53
		13151	1.655		37.73
		13543	1.704		35.87
粗砂	0.50<d≤2.00	12005	1.510	2.630	42.57
		12152	1.529		41.87
		13569	1.707		35.09
		13673	1.720		34.59
		14673	1.846		29.81

下载: 导出CSV 

| 显示表格

众所周知，等径颗粒砂的孔隙度只与其排列方式有关，与粒径大小无关。不等粒砂的孔隙度大小与其分选性、排列方式等多个因素有关。本次试验采用3个粒级的砂样，都是市场通用的分选性较好的“近等粒”砂，即可以近似地认定为等径颗粒砂样。同一种砂人工捣实强度不同，压实度不同。颗粒排列方式变化，引起的孔隙度存在0.3～0.5倍的差异，而渗透性却产生2～3倍的差异。

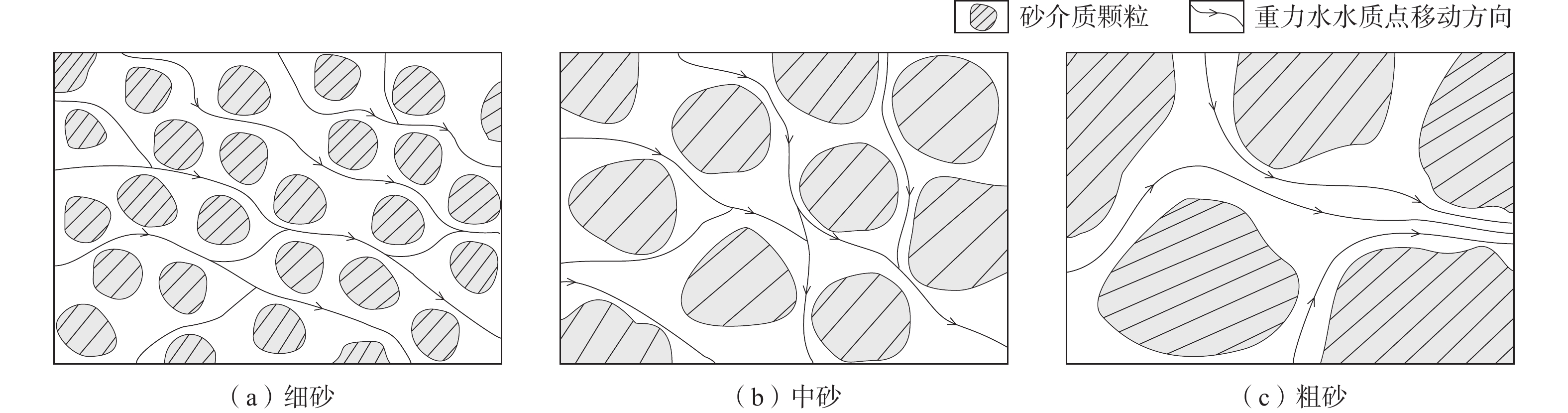
究其原因，应该与孔隙大小有关。孔隙度相同或相近的等径砂介质内部包含的孔隙体积相同或相近，但是砂粒间孔隙尺寸却随着粒径的增大而增大，相应孔隙数量减少，见图9。由此看出，平均孔隙尺寸的增大，使得允许水通过的断面增大；孔隙数量的减少，使得水绕流的路程缩短；两者效应的结果，水头损失降低，单位时间的渗流量增大，渗透系数增大。

图  9  水在不同粒径砂介质中的运动状态模型

Figure  9.  Models of the water motion state in a sand medium with different particle sizes

下载: 全尺寸图片 幻灯片

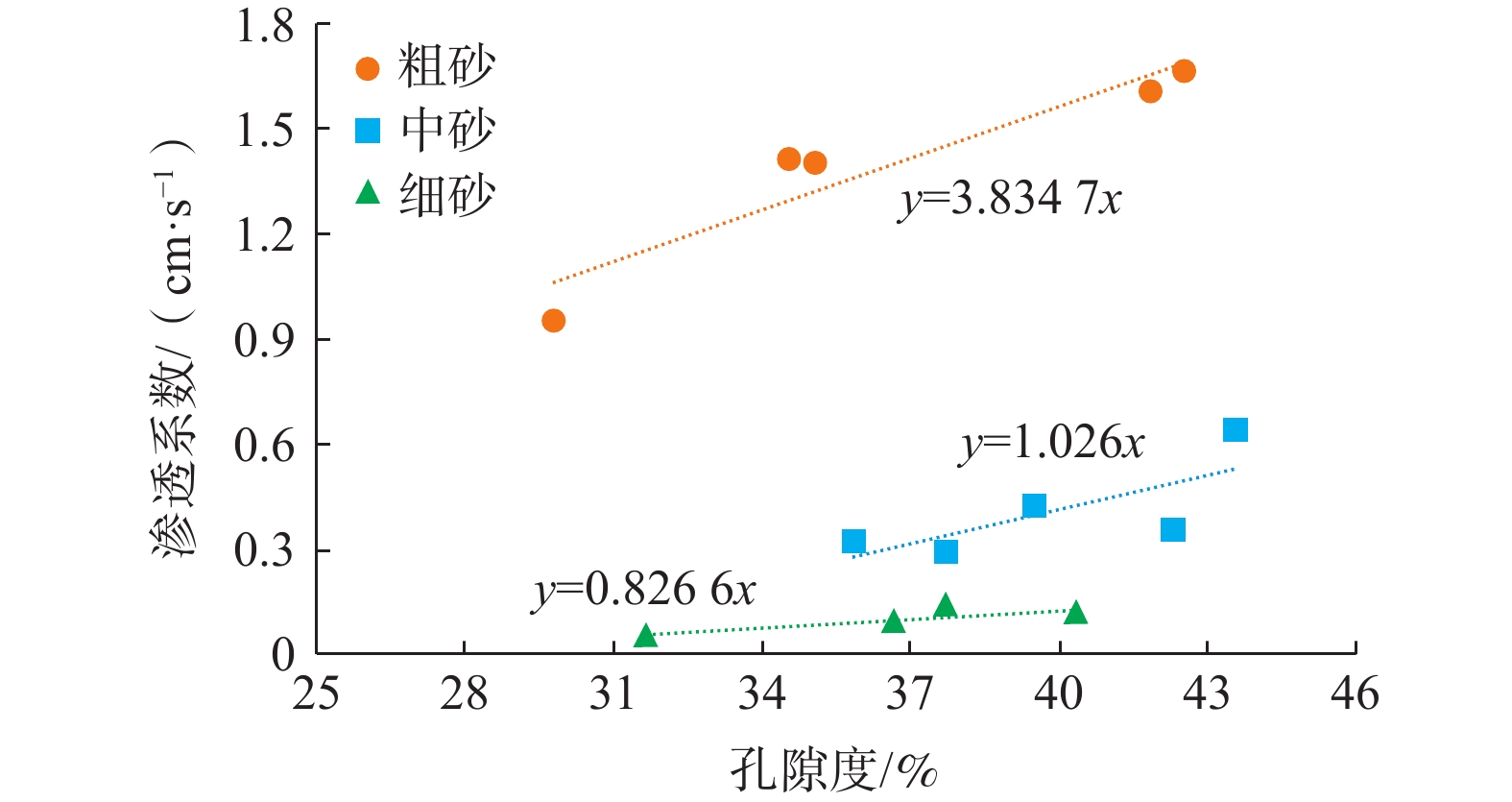
不同孔隙度与试验测得的渗透系数，见图10。可以看出：同一粒径，渗透系数随孔隙度增大而增大；不同粒径之间，尤其是在相同压实度情况下，孔隙度差别不大，渗透系数却显著不同，粒径越大，渗透系数明显增大。当渗透系数相同时，粒径越小，孔隙度越大，反之亦然。

图  10  不同砂介质的渗透系数与孔隙度的线性关系

Figure  10.  Linear relationships between the hydraulic conductivity and the porosity in different sand media

下载: 全尺寸图片 幻灯片

3.   讨论

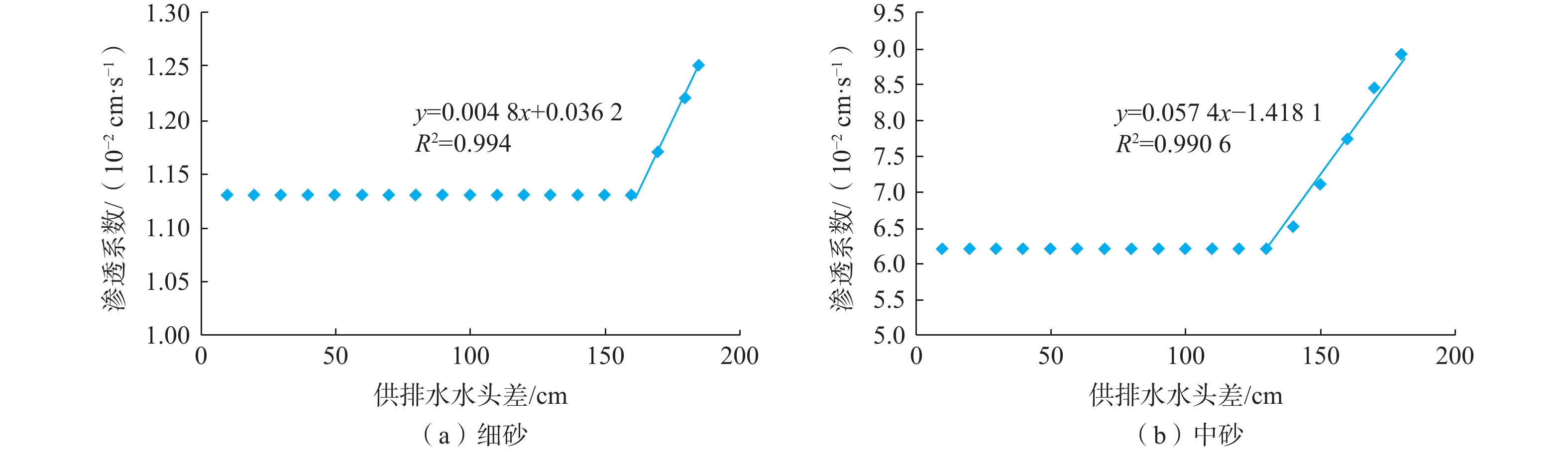
当介质为细砂时，稳水室高度（H_w）达到223 cm、供排水水头差（H）为170 cm时，测压孔F1～F4间水头差开始下降，水力坡度也开始下降，渗透流速先缓慢下降、而后盘桓上升。随着H_w继续升高、H继续增大，测压孔F1～F4间水头差出现波动，水力坡度与渗透流速随之波动，呈现不规则的螺旋式的变化，见图6（a）。

当介质为中砂时，稳水室高度达到193 cm、供排水水头差为140 cm时，测压孔F1～F4间水头差从51.1 cm开始下降，水力坡度从1.4194 cm/s开始下降，但渗透流速先是波动，而后缓慢增加。当H_w达到233 cm、H为180 cm时，测压孔F1～F4间水头差下降了11.9 cm，渗透流速在这期间升高了0.0096 cm/s，达到0.1023 cm/s，见图6（b）。

细、中砂的供排水水头差与相应的平均渗透系数的关系，见图11。渗透系数的值在出现异常前为一常数，数值上等于渗透流速与水力坡度的关系直线的斜率，细砂为1.13×10⁻² cm/s，中砂为6.19×10⁻² cm/s。但当供排水水头差达到一定值以后，渗透系数的值发生波动和变化，总体呈现急剧增加，其趋势依然呈现良好线性增加。也就是说，异常出现前，渗透系数不受供排水水头差影响；异常出现后，渗透系数的值随着供排水水头差的增加而增加。

图  11  细、中砂渗透系数随供排水水头的变化

Figure  11.  Changes of the hydraulic conductivity in the fine and medium sands

下载: 全尺寸图片 幻灯片

通常认为，当水流流线相互平行时，渗流可以看作层流，此时渗流运动规律符合达西定律，雷诺数Re为小于1~10之间的某一数值。

本次试验用砂选用标准实验室用石英砂，因此可将砂介质看作理想的等径圆球颗粒，其平均粒径近似地视为圆球粒直径（D）。众所周知，当颗粒为立方体排列时，其最大空隙（d_max）为0.732D，其最小空隙（d_min）也达到0.414D；颗粒呈其他排列方式时，其最大最小空隙将相应减小，以四面体排列为最小。但是自然界里通常既不是四分体排列也不是四面体排列，所以将平均粒径的一半（0.5D）作为空隙的大小。雷诺数表达为：

式中：θ——多孔介质中颗粒的有效通过孔隙；

$\mu$——水的运动黏性系数/（cm²·s⁻¹）。

试验中，环境温度保持在18～25 °C，水温与环境温度基本一致，因此水的运动黏性系数取0.01 cm²/s。

经计算分析发现，细砂在雷诺数Re≥0.4时出现紊乱，中砂在雷诺数Re≥3.3时出现紊乱。细砂与中砂在试验中出现的异常情况，是由于渗透流速达到了达西定律所遵循的临界条件造成的。水流从线性运动变为非线性运动，进一步向紊流过渡。

4.   结论

（1）在常压下，随着温度升高，砂介质渗透系数逐步增大，且渗透性越好，升高的速度越快。

（2）在常温常压下，随着TDS增大，砂介质渗透系数变小。渗透性好的介质，其渗透系数随TDS呈幂函数或指数函数变化，即在低TDS变化时引起的介质的渗透系数的变化剧烈，反之亦然；而渗透性差的介质，渗透性随着TDS的增高近似呈线性减小。

（3）同一种砂介质在常温条件下，供排水水头差增大，给予的水压能量变大，渗透流速逐步增大，但渗透系数增速产生波动或在某区间内保持不变。本次测定出细砂临界雷诺数为0.4，中砂临界雷诺数为3.3。

（4）砂介质的粒径和压实度亦是渗透系数重要影响因素之一，同一粒径砂介质压实度越高，渗透系数越低，导水性能下降；不同粒径砂介质，孔隙度相同时，粒径越大渗透系数越大。

水和砂介质的状态对渗透性的影响十分复杂。本次试验研究存在一些不足：本次试验仅涉及了3种粒径的砂，其他粒径或不同粒径组合的砂的情况，有待进一步试验验证；本试验根据达西试验的原理，设计采用了供水稳水室高度可变、但仍然是恒定供排水水头差的类达西试验装置，简单直观，但未能减少人为的误差对试验结果的影响。尤其是装置没有隔热功能，变化温度的试验存在的误差较大，今后可以设计更为精密的试验进一步验证。